Study of C₁^T.

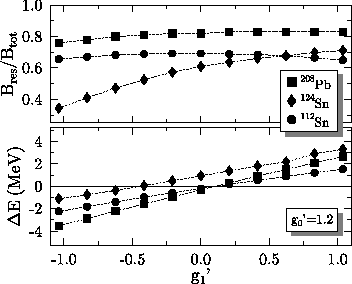
Figure 10: Variation of the GT resonance energy and the strength in the resonance when C₁^T (and thus g₁') is varied. C₁^s is readjusted for each value of C₁^T so that g₀' = 1.2. Symbols and scales are as in Fig. 6.

Finally, we investigate the influence on the GT strength distribution of the term $C_1^T \vec{s}_{1t_3} \cdot \vec{T}_{1t_3}$, which determines g₁' [see Eq. (18)]. As this term is linked by gauge invariance (11) to the time-even $\stackrel{\leftrightarrow}{J}^2_1$ term, a fully self-consistent variation of C₁^T would require refitting the whole time-even sector of the Skyrme functional. (Note that our approach removes the constraints (34) that link C_t^T to the time-even coupling constants $C_t^\tau$ and $C_t^{\Delta \rho}$. The constraint was retained, however, when Sk0' was constructed.) We leave that task for the future, using a gauge-invariance breaking-energy functional here with $C_1^T \neq C_1^J$ to obtain constraints on C₁^T for future fits. Figure 10 shows the change in the GT resonance when g₁' is varied in the range $-1 \leq g_1' \leq 1$. Increasing g₁' increases the energy of the GT resonance for a given g₀'. Changing g₁' by 0.2 has nearly the same effect on the GT resonance energy as changing g₀' by 0.2. (This means that g₀'=1.2, g₁'=0.2, as used here, is consistent with the lower end of the values $1.4 \leq g_0' \leq 1.6$, g₁'=0.0 given in [45,46,47,48].) As the curves for ²⁰⁸Pb and ¹¹²Sn demonstrate, however, the amount of strength in the resonance does not necessarily change when g₁' is varied.