The Skyrme energy functional

Within the local-density approximation, the energy functional is given by the spatial integral of the local energy density ${\cal H}(\vec{r})$

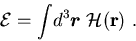$${\cal E} = \int \! d^3 \mbox{{\boldmath {$r$}}} \; {\cal H}(\vec{r})~.$$ (4)

The energy density is composed of the kinetic term ${\cal H}_{\rm kin}$, the Skyrme energy density ${\cal H}_{\rm Skyrme}$ that describes the effective strong interaction between the nucleons, and a term arising from the electromagnetic interaction ${\cal H}_{\rm em}$:

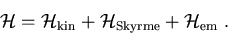$${\cal H} = {\cal H}_{\rm kin} + {\cal H}_{\rm Skyrme} + {\cal H}_{\rm em} ~.$$ (5)

For the electromagnetic interaction, we take the standard Coulomb expression, including the Slater approximation for the exchange term. The energy functional discussed here contains all possible terms bilinear in local densities and currents and up to second order in the derivatives that are invariant under reflection, time-reversal, rotation, translation, and isospin rotation [20].

Time-reversal invariance requires the energy density to be bilinear in either time-even densities or time-odd densities, so the Skyrme energy density can be separated into a ``time-even" part ${\cal H}^{\rm even}$ and a ``time-odd" part ${\cal H}^{\rm odd}$:

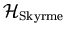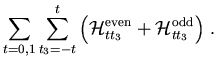$${\cal H}_{\rm Skyrme} \sum_{t = 0,1} \sum_{t_3 = -t}^{t} \Big( {\cal H}_{t t_3}^{\rm even} + {\cal H}_{t t_3}^{\rm odd} \Big) ~.$$ = (6)

The sum runs over the isospin t and its third component t₃. Only the t₃ = 0 component of the isovector t = 1 terms contribute to nuclear ground states and the rotational bands discussed later, while the $t_3 = \pm 1$ components contribute only to charge-exchange (e.g. GT) excitations. In the notation of Refs. [3,20], the time-even and time-odd Skyrme energy densities read

$${\cal H}_{t t_3}^{\rm even}\! C_t^{\rho} \, \rho_{t t_3}^{2} + C_t^{\Delta \rho} \, \rho_{t t_3} \Delta \rho_{t t_3} + C_t^{\tau} \, \rho_{t t_3} \tau_{t t_3}$$ =

$$C_t^{\nabla J} \rho_{t t_3} \, \nabla \cdot \vec{J}_{t t_3} + C_t^{J} \stackrel{\leftrightarrow}{J}^2_{t t_3},$$ + (7)

$${\cal H}_{t t_3}^{\rm odd}\! C_t^{s} \, \vec{s}^{2}_{t t_3} + C_t^{\Delta s} \, \vec{s}_{t t_3} \cdot \Delta \vec{s}_{t t_3} + C_t^{T} \, \vec{s}_{t t_3} \cdot \vec{T}_{t t_3}$$ =

$$C_t^{\nabla s} \, (\nabla \cdot \vec{s}_{t t_3})^2 + C_t^{j} \, \... ...3} + C_t^{\nabla j} \, \vec{s}_{t t_3} \cdot \nabla \times \vec{j}_{t t_3}.\!\!$$ + (8)

Isospin invariance of the Skyrme interaction makes the coupling constants independent of the isospin z-projection. All coupling constants might be density dependent. Following the standard ansatz for the Skyrme interaction, we neglect such a possibility except in $C_t^{\rho}$ and C_t^s, for which we restrict the density dependence to the following form

$$C_t^{\rho} [\rho_0] C_1^{\rho}[0] + \Big(C_1^{\rho}[\rho_{\rm nm}]-C_1^{\rho}[0]\Big) \left( \frac{\rho_0}{\rho_{\rm nm}} \right)^{\alpha}~,$$ = (9)

$$C_t^{s} [\rho_0] C_1^{s}[0] + \Big(C_1^{s}[\rho_{\rm nm}]-C_1^{s}[0]\Big) \left( \frac{\rho_0}{\rho_{\rm nm}} \right)^{\xi} .$$ = (10)

Here $\rho_0$ is the isoscalar scalar density, and $\rho_{\rm nm}$ is its value in saturated infinite nuclear matter. The exponent $\alpha$ that specifies the density dependence of $C_t^{\rho} [\rho_0]$ must be about 0.25 for the incompressibility coefficient $K_\infty$ to be correct[21,22,23,24]. Although this fact does not restrict the analogous power in $C_t^{s} [\rho_0]$, Eq. (10), we keep $\xi$ equal to $\alpha$ for simplicity here. Usually we will consider energy functionals that are invariant under local gauge transformations [3], which generalize the Galilean invariance of the Skyrme interaction discussed in [2]. Gauge invariance links three pairs of time-even and time-odd terms in the energy functional:

$$- C_t^{\tau} \quad , \quad C_t^{J} = - C_t^{T} \quad , \quad C_t^{\nabla j} = + C_t^{\nabla J} ~,$$ C_t^j = 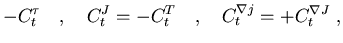(11)

These relations fix all orbital time-odd terms, leaving only time-odd terms corresponding to the spin-spin interaction with free coupling constants. Relations (11) lead to a simplified form of Eqs. (6)-(8),

$${\cal H}_{\rm Skyrme} \sum_{t = 0,1} \sum_{t_3 = -t}^{t} \Big[ C_t^{\rho} \, \rho_{t t_3}^{2} + C_t^{s} \, \vec{s}^{2}_{t t_3}$$ =

$$C_t^{\Delta \rho} \, \rho_{t t_3} \Delta \rho_{t t_3} + C_t^{\Delta s} \, \vec{s}_{t t_3} \cdot \Delta \vec{s}_{t t_3}$$ +

$$C_t^{\tau} \, ( \rho_{t t_3} \tau_{t t_3} - \vec{j}^2_{t t_3} ) +... ...ec{s}_{t t_3} \cdot \vec{T}_{t t_3} - \stackrel{\leftrightarrow}{J}^2_{t t_3} )$$ +

$$C_t^{\nabla J} \, ( \rho_{t t_3} \, \nabla \cdot \vec{J}_{t t_3} + \vec{s}_{t t_3} \cdot \nabla \times \vec{j}_{t t_3} )$$ +

$$C_t^{\nabla s} \, (\nabla \cdot \vec{s}_{t t_3})^2 \Big] \quad .$$ + (12)

The time-even terms of the energy functional can be directly related to nuclear bulk properties such as E/A, the saturation density $\rho_{\rm n.m.}$, incompressibility, symmetry energy, surface and surface symmetry energy, and spin-orbit splittings. The remaining time-odd terms cannot.

We will set the coupling constant $C_t^{\nabla s}$ to 0. The term it multiplies comes from a local two-body tensor force considered in Skyrme's original papers [25] and discussed by Stancu et al. [26], but omitted in all modern Skyrme parameterizations except the force SL1 introduced by Liu et al. [27], which has not been used since.