


Next: Time-reversal, and signature or
Up: Single-particle bases for conserved
Previous: Parity
Time-reversal, and T-signature or T-simplex
For operators
 ,
for which both Eq. (11) and (15) hold,
matrix
,
for which both Eq. (11) and (15) hold,
matrix  in Eq. (13) can be additionally simplified,
and reads
in Eq. (13) can be additionally simplified,
and reads
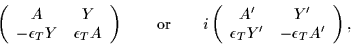 |
(23) |
for
 =+1 and
=+1 and
 =-1, respectively,
where all submatrices are real, A is symmetric, A' is
antisymmetric,
=-1, respectively,
where all submatrices are real, A is symmetric, A' is
antisymmetric,
 =
=
 ,
and
,
and
 =
=
 .
.
In particular, with
 =
=
 =+1, the matrix from
Eq. (23) reduces to
=+1, the matrix from
Eq. (23) reduces to
 |
(24) |
where A is symmetric, Y antisymmetric, and both are real.
In order to diagonalize such matrix, one can consider a smaller problem,
by constructing a complex matrix
 =A-iY
which has the size twice smaller than the
original matrix
=A-iY
which has the size twice smaller than the
original matrix  .
After diagonalizing
.
After diagonalizing
 ,
and separating
real and imaginary parts of its complex eigenvectors,
,
and separating
real and imaginary parts of its complex eigenvectors,
 |
(25) |
one gets two degenerate real eigenvectors of  :
:
 and
and
 .
If
.
If
 is the mean-field Hamiltonian, such a form of eigenvectors simplifies
expressions for densities.
is the mean-field Hamiltonian, such a form of eigenvectors simplifies
expressions for densities.



Next: Time-reversal, and signature or
Up: Single-particle bases for conserved
Previous: Parity
Jacek Dobaczewski
2000-02-05
![]() ,
for which both Eq. (11) and (15) hold,
matrix
,
for which both Eq. (11) and (15) hold,
matrix ![]() in Eq. (13) can be additionally simplified,
and reads
in Eq. (13) can be additionally simplified,
and reads
![]() =
=
![]() =+1, the matrix from
Eq. (23) reduces to
=+1, the matrix from
Eq. (23) reduces to
 and
and
 .
If
.
If