Parity

Standard simplification always occurs for operators which are even with respect to the parity operator $\hat{\cal{P}}$,

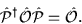$$\hat{\cal{P}}^\dagger\hat{\cal{O}}\hat{\cal{P}}= \hat{\cal{O}}.$$ (22)

All matrices and submatrices introduced above or below acquire a block-diagonal form, provided the single-particle bases consist of states with well defined parity (such as, e.g., bases listed in Tables 3 or 4). Therefore, apart from Sec. 3.1.7, we do not separately discuss cases when the parity is one of the conserved D $_{\mbox{\rm\scriptsize {2h}}}^{\mbox{\rm\scriptsize {TD}}}$ operators, and we note that the effect of the parity conservation can be easily included on top of any other symmetry conditions.