


Next: T-signature or T-simplex
Up: Single-particle bases for conserved
Previous: Single-particle bases for conserved
Time-reversal
Let us first consider operators
 which are either even (invariant)
or odd (antiinvariant) with respect to the time-reversal:
which are either even (invariant)
or odd (antiinvariant) with respect to the time-reversal:
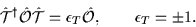 |
(11) |
From Eqs. (9) and (11) one gets
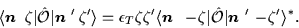 |
(12) |
It follows, that the matrix corresponding to
 reads
reads
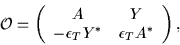 |
(13) |
where A is hermitian, and Y is antisymmetric
or symmetric for
 =+1 and
=+1 and
 =-1, respectively.
No block-diagonal structure appears, nevertheless, only two
instead of four
submatrices, A and Y, complex in general, have to be calculated.
=-1, respectively.
No block-diagonal structure appears, nevertheless, only two
instead of four
submatrices, A and Y, complex in general, have to be calculated.
Jacek Dobaczewski
2000-02-05
![]() which are either even (invariant)
or odd (antiinvariant) with respect to the time-reversal:
which are either even (invariant)
or odd (antiinvariant) with respect to the time-reversal: