Study of C₁^s [0].

Thus far we have chosen not to let C₁^s depend on the density. Little is known about the empirical density dependence of the time-odd energy functional, and time-odd Landau parameters calculated from a ``realistic'' one-boson exchange potential in DBHF show only a very weak density dependence [64]. Because the kinetic spin term $C_1^T \vec{s}_{1t_3} \cdot \vec{T}_{1t_3}$, when evaluated in INM, also contributes to the density dependence of the Landau parameters, the density-dependence of that term must either be small or nearly canceled by other time-odd terms. In any event, in the following, we investigate what happens when C<sub>1</sub><sup>s</sup> depends on the (isoscalar) density in the ``standard" way (10). All nuclei we look at have finite neutron excess, which means that the central density should be slightly smaller than $\rho_{\rm nm}$.

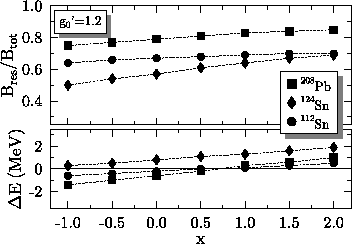
Figure 8: Variation of the GT resonance energy and the strength in the resonance when the ratio x$\equiv$C₁^s[0]/ $C_1^{s} [\rho _{\rm nm}]$ of parameters defining the density dependence of $C_1^{s} [\rho]$ in Eq. (10) is varied. Symbols and scales are as in Fig. 6.

If g₀' and g₁' are fixed in saturated INM, there is one free parameter, C₁^s[0], with which one can vary the density dependence (10). ( $C_1^{s} [\rho _{\rm nm}]$ is fixed by the value $g_0'[\rho_{\rm nm}]$=1.2, and we set the exponent $\xi$=0.25, as it is in the time-even energy functional SkO'.) We continue here to assume that gauge invariance holds, and that $C_1^{\Delta s} = 0$.

We vary the parameter C₁^s[0] between $-C_1^{s}[\rho_{\rm nm}]$ and $2C_1^{s}[\rho_{\rm nm}]$. Figure 7 shows the spatial dependence of $C_1^{s} [\rho]$ for several values of the ratio x$\equiv$C₁^s[0]/ $C_1^{s} [\rho _{\rm nm}]$. By changing C₁^s[0], one can change both the GT resonance energy and the amount of the low-lying strength, even with $g_0'[\rho_{\rm nm}]$ kept constant. As Fig. 8 shows, an increase of C₁^s[0] for a given g₀' has almost the same effect as an increase of g₀' for a given C₁^s[0]. Thus, the INM Landau parameters do not tell the whole story in a finite nucleus. Figures 7 and 8 show that the spin-spin coupling has the largest effect on the GT resonance when it is located at or even slightly outside the nuclear radius.