Nonlocal energy density functionals for low-energy nuclear structure

F Raimondi, K Bennaceur, J Dobaczewski

Abstract:

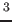
We introduce a finite-range pseudopotential built as an expansion in derivatives up to next-to-next-to-next-to-leading order (N$^3$LO) and we calculate the corresponding nonlocal energy density functional (EDF). The coupling constants of the nonlocal EDF, for both finite nuclei and infinite nuclear matter, are expressed through the parameters of the pseudopotential. All central, spin-orbit, and tensor terms of the pseudopotential are derived both in the spherical-tensor and Cartesian representation. At next-to-leading order (NLO), we also derive relations between the nonlocal EDF expressed in the spherical-tensor and Cartesian formalism. Finally, a simplified version of the finite-range pseudopotential is considered, which generates the EDF identical to that generated by a local potential.