Parametrization of the LST functions

 

In principle, we could use the flexibility of having three different LST functions f_k(r) and three different oscillator lengths L_k of the original deformed HO basis to tailor the LST transformation to the shape of the deformed nucleus under investigation. However, for large HO bases (in the present study we include HO states up to 20 major shells), the dependence of the total energy on the basis deformation is very weak, so that minimization of the total energy with respect to the three oscillator lengths L_k is ill-conditioned (see discussion and examples given in Ref. [15]). Therefore, in this study, we use a spherical HO basis depending on a single common oscillator length L₀,

$$L_x=L_y=L_z \equiv L_0= \frac{1}{b_0}=\sqrt{\frac{\hbar}{m\omega_{0}}}.$$ (13)

With such a choice, it is natural to set the three LST functions f_k(r) equal to one another,

$$f_x({r})=f_y({r})=f_z({r}) \equiv f({r}).$$ (14)

This allows us to use exactly the same LST function f(r) as in the previous studies [10,11]. Under conditions (14), the Jacobian (3) assumes the simpler form

 

$$\equiv \frac{\partial(x^{\prime},y^{\prime},z^{\prime})}{\partial(x,y,z)} = \frac{f^{\prime}({r})f^2({r})}{{r}^{2}}.$$ D 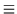(15)

The parametrization of the LST function f(r) used in Refs. [10,11] was of the form

$$f({r})=L_0 F\left(\frac{r}{L_0}\right),$$ (16)

with the dimensionless universal function F of the dimensionless variable ${\cal R}$ defined as

$$F({\cal R})\!=\!\left\{\!\! \begin{array}{lll} {\cal R}\left(... ...}\ln {\cal R}} & \mbox{for} & {\cal R}>c\;. \end{array}\right.$$ (17)

Two different formulae can be obtained for the function $F({\cal R})$, one for ${\cal R}\leq c$ and one for ${\cal R}>c$. Imposing the condition that the function should be continuous at the matching radius c and that it should have continuous first, second, third, and fourth derivatives leads to the following requirements for the constants d_-2, d_-1, d₀, d₁, and d_L:

$$\begin{tabular}{l@{}l@{}l} $d_{-2}$\space & = & $\frac{1}{3}{... ...^{2}} +6090 {\gamma ^{3}}+1820 {\gamma ^{4}}} ) ,$\end{tabular}$$ (18)

where ${\gamma}$=ac² and ${\cal A}^{-1}$= ${81 {{\left( 1+\gamma \right)} ^{10/3}}}$. In this way, the LST function f(r) is guaranteed to be very smooth, while still depending on only three parameters, L₀, a and c.

From (17), we see that asymptotically the function $F({\cal R}$ $\rightarrow$$\infty)$$\sim$ $\sqrt{d_1 {\cal R}}$. Thus, the LST function obeys conditions (11) provided that the parameters satisfy

$$\kappa=\frac{d_1}{2L_0}.$$ (19)

Two different approaches can be used in calculations. One possibility is to minimize the total energy with respect to L₀, a, and c, obtaining as output the energetically optimal value of the decay constant $\kappa$. Alternatively, for a given choice of $\kappa$, we could eliminate one of the three parameters and minimize the total energy with respect to the other two. The actual procedure used in our calculations is described in Sec. 4.1.