Axially deformed harmonic oscillator

 

In the present study, we restrict our HFB analysis to shapes having axial symmetry. For this purpose, we use HO wave functions in cylindrical coordinates, z, $\rho$, and $\varphi$,

$$\begin{array}{lll} x & = & \rho \cos \varphi \;, \\ y & = & \rho \sin \varphi \;, \\ z & = & z\;, \end{array}$$ (20)

which allows us to separate the HFB equations into blocks with good projection $\Omega$ of the angular momentum on the symmetry axis. [Note that the use of cylindrical coordinates is independent of working with equal oscillator lengths (13).] Since the use of a cylindrical HO basis is by now a standard technique (see, e.g., Ref. [16]), we give here only the information pertaining to constructing the cylindrical THO states.

The cylindrical HO basis wave functions are given explicitly by

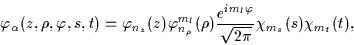$$\varphi_{\alpha}(z,\rho,\varphi,s,t)= \varphi_{n_{z}}(z)\varp... ...{im_{l}\varphi}}{\sqrt{2\pi}}\chi _{m_{s}}(s)\chi _{m_{t}}(t),$$ (21)

where the spin s and isospin tdegrees of freedom are shown explicitly, n_z and $n_{\rho}$ are the number of nodes along z and $\rho$ directions, respectively, while m_l and m_sare the components of the orbital angular momentum and the spin along the symmetry axis. The only conserved quantum numbers in this case are the total angular momentum projection $\Omega$=m_l+m_s and the parity $\pi$= (-)^n_z+m_l.

In the axially deformed case, the general LST (1) acts only on the cylindrical coordinates z and $\rho$ and takes the form

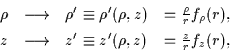$$\begin{array}{llll} \rho & \longrightarrow & \rho^{\prime}\eq... ...quiv z^{\prime}(\rho,z) & = \frac{z}{{r}} f_z({r}), \end{array}$$ (22)

with the corresponding Jacobian given by

 

$$\equiv \frac{\partial(x^{\prime},y^{\prime},z^{\prime})}{\partial(x,y,z)} = \frac{\rho^2f^{\prime}_\rho f_\rho f_z + z^2f^2_\rho f^{\prime}_z}{{r}^{4}} .$$ D 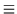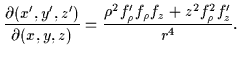(23)

Finally, the axial THO wave functions are

 

$$\psi_{\alpha}(z,\rho,\varphi,s,t) D^{1/2}\textstyle{\ \varphi_{n_{z}}\left(\frac{z}{{r}}f_z({r})\right) \varphi_{n_{\rho }}^{m_{l}}\left(\frac{\rho }{{r}}f_\rho({r})\right)}$$ =

$$\times \frac{e^{im_{l}\varphi}}{\sqrt{2\pi}}\chi _{m_{s}}(s)\chi _{m_{t}}(t).$$ (24)

The assumption of a single oscillator length (see Sect. 2.3) that we make in our calculations translates in the axial case to

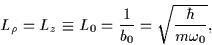$$L_\rho=L_z \equiv L_0=\frac{1}{b_0}=\sqrt{\frac{\hbar}{m\omega_{0}}},$$ (25)

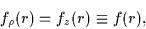$$f_\rho({r})=f_z({r}) \equiv f({r}),$$ (26)

and the Jacobian (23) reduces to expression (15).