Transformed harmonic oscillator wave functions

 

The anisotropic three-dimensional HO potential with three different oscillator lengths

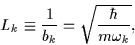$$L_{k} \equiv \frac{1}{b_k}=\sqrt{\frac{\hbar}{m\omega_{k}}},$$ (5)

has the form

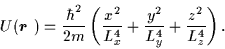$$U({\mbox{{\boldmath {$r$ }}}})=\frac{\hbar^2}{2m}\left( \frac... ...}} +\frac{y^{2}}{ L_{y}^{4}} +\frac{z^{2}}{L_{z}^{4}}\right) .$$ (6)

Its eigenstates, the separable HO single-particle wave functions

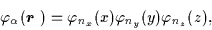$$\varphi_{\alpha}({\mbox{{\boldmath {$r$ }}}})=\varphi _{n_{x}}(x)\varphi _{n_{y}}(y) \varphi _{n_{z}}(z) ,$$ (7)

have a Gaussian asymptotic behavior at large distances,

$$\varphi _{\alpha}({\mbox{{\boldmath {$r$ }}}\rightarrow \inft... ...c{y^{2}}{L_{y}^{2}} +\frac{z^{2}}{L_{z}^{2}} \right) \right] .$$ (8)

Applying the LST (1) to these wave functions leads to the so-called THO single-particle wave functions (4),

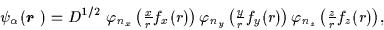$$\psi_{\alpha}({\mbox{{\boldmath {$r$ }}}})=D^{1/2}\textstyle{... ...\right) \varphi _{n_{z}}\left( \frac{z}{{r}}f_z({r)}\right)} ,$$ (9)

whose asymptotic behavior is

$$\psi_{\alpha}({\mbox{{\boldmath {$r$ }}}\rightarrow\infty })\... ...y}^{2}r^2} + \frac{z^{2}f^2_z}{L_{z}^{2}r^2} \right) \right] .$$ (10)

This suggests that we choose the LST functions to satisfy the asymptotic conditions

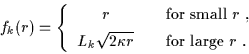$$f_k(r) = \left\{ \begin{array}{cl} r & \mbox{~~~for small $r$... ...sqrt{2\kappa r} & \mbox{~~~for large $r$ }. \end{array}\right.$$ (11)

With such a choice, the THO wave functions at small r are identical to the HO wave functions (note that with (11) one obtains D=1 at small r), while at large r they have the correct exponential and spherical asymptotic behavior,

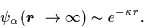$$\psi _{\alpha}({\mbox{{\boldmath {$r$ }}}\rightarrow \infty })\sim e^{-\kappa r}.$$ (12)