


Next: Transition energy density
Up: Particle-Number Projection and the
Previous: Poles of transition densities
Particle-Number-Projected DFT
According to the DFT, the energy density
of the system,
 , can be written as a function of
the local particle
, can be written as a function of
the local particle  and pairing
and pairing  densities obtained as the diagonal elements of the corresponding density
matrices:
densities obtained as the diagonal elements of the corresponding density
matrices:
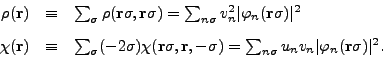 |
(30) |
The nuclear density functionals for time-even systems also depend
on kinetic  and spin-orbit
and spin-orbit  densities. An even
larger set of densities enters the energy density for
time-odd systems
[38,13]. For simplicity, we discuss here the
dependence on the particle density only, because extension to other
densities is straightforward.
densities. An even
larger set of densities enters the energy density for
time-odd systems
[38,13]. For simplicity, we discuss here the
dependence on the particle density only, because extension to other
densities is straightforward.
We note in passing that the densities corresponding
to the shifted HFB state
 (6) can be written as:
(6) can be written as:
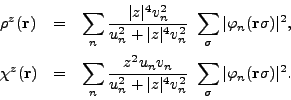 |
(31) |
Subsections
Jacek Dobaczewski
2007-08-08
![]() , can be written as a function of
the local particle
, can be written as a function of
the local particle ![]() and pairing
and pairing ![]() densities obtained as the diagonal elements of the corresponding density
matrices:
densities obtained as the diagonal elements of the corresponding density
matrices:
![]() (6) can be written as:
(6) can be written as: