


Next: Projected HFB states
Up: Particle-Number-Projected HFB
Previous: Particle-Number-Projected HFB
Shifted HFB states
Let us introduce several useful notations that will be used later.
First, we call the operator appearing under the integral (2)
the shift operator,
 |
(3) |
parametrized by means of a single complex number  ,
,  =
= .
The shift operator
.
The shift operator  is parametrized by the
complex number
is parametrized by the
complex number  and constitutes
a non-unitary Bogoliubov transformation (in fact, a non-unitary single-particle
basis transformation) of simple kind, i.e.,
and constitutes
a non-unitary Bogoliubov transformation (in fact, a non-unitary single-particle
basis transformation) of simple kind, i.e.,
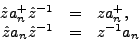 |
(4) |
or
 |
(5) |
Obviously, for  , the shift operator is equal to identity.
, the shift operator is equal to identity.
Second, we define the shifted HFB states as
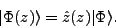 |
(6) |
When the HFB state  is expressed through the
Thouless theorem [1] (we assume an even number of
particles for simplicity),
is expressed through the
Thouless theorem [1] (we assume an even number of
particles for simplicity),
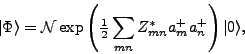 |
(7) |
the shifted HFB states read
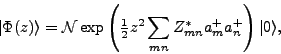 |
(8) |
where  is the normalization constant of the HFB state (7).
Similarly, for the HFB state expressed in the canonical basis
or for a BCS state,
is the normalization constant of the HFB state (7).
Similarly, for the HFB state expressed in the canonical basis
or for a BCS state,
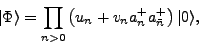 |
(9) |
the shifted state reads
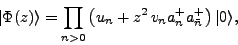 |
(10) |
where  and
and  are the real HFB occupation amplitudes in the canonical
basis and the product
are the real HFB occupation amplitudes in the canonical
basis and the product  involves only one state from each
pair of canonical partners (see Ref. [1] for details).
involves only one state from each
pair of canonical partners (see Ref. [1] for details).
We call  a shift, because it moves the HFB state
a shift, because it moves the HFB state
 =
=
 from its original position at
from its original position at
 to a different point
to a different point  in the complex plane. Since
consecutive shift transformations correspond to products of the shift
parameters
in the complex plane. Since
consecutive shift transformations correspond to products of the shift
parameters  , the parameters
, the parameters  and
and  in Eq. (3)
are additive.
in Eq. (3)
are additive.



Next: Projected HFB states
Up: Particle-Number-Projected HFB
Previous: Particle-Number-Projected HFB
Jacek Dobaczewski
2007-08-08
![]() a shift, because it moves the HFB state
a shift, because it moves the HFB state
![]() =
=
![]() from its original position at
from its original position at
![]() to a different point
to a different point ![]() in the complex plane. Since
consecutive shift transformations correspond to products of the shift
parameters
in the complex plane. Since
consecutive shift transformations correspond to products of the shift
parameters ![]() , the parameters
, the parameters ![]() and
and ![]() in Eq. (3)
are additive.
in Eq. (3)
are additive.