


Next: Particle-Number-Projected DFT
Up: Particle-Number-Projected HFB
Previous: Transition matrix elements and
Poles of transition densities
It is seen immediately from Eq. (27) that
the transition density matrices have imaginary axis poles at
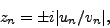 |
(28) |
and, therefore, are not analytical. These poles carry over to the HFB
transition energy density as well. The poles appear beyond the origin,
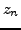
 0, provided all amplitudes
0, provided all amplitudes  are nonzero; we assume this
hereafter, i.e., none of the canonical states is being blocked. We can
also safely assume that all amplitudes
are nonzero; we assume this
hereafter, i.e., none of the canonical states is being blocked. We can
also safely assume that all amplitudes  are nonzero, because
otherwise the corresponding states would not contribute to the density
matrices at all. Of course, if there exist poles in the HFB transition
energy density, they must be cancelled by the norm overlap
are nonzero, because
otherwise the corresponding states would not contribute to the density
matrices at all. Of course, if there exist poles in the HFB transition
energy density, they must be cancelled by the norm overlap
 , because the Hamiltonian matrix element
, because the Hamiltonian matrix element
 is an analytical function of
is an analytical function of  .
.
However, as we discuss in the next section, whenever the transition
energy density is not related to a Hamiltonian, or some approximations are
involved in Hamiltonian's construction, the presence of the poles
(28) requires special
attention. For example, the exact HFB transition energy density,
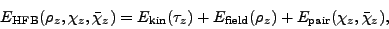 |
(29) |
is often split into the kinetic term
 that
depends on the kinetic transition density, the mean-field term
that
depends on the kinetic transition density, the mean-field term  that depends on the particle transition density, and the
pairing term
that depends on the particle transition density, and the
pairing term  that depends on the pairing transition
densities. It was first realized in Ref. [30],
and then discussed by several authors
[31,32,37], that the poles
are not
cancelled separately in
that depends on the pairing transition
densities. It was first realized in Ref. [30],
and then discussed by several authors
[31,32,37], that the poles
are not
cancelled separately in  and
and  , but only in the sum thereof, i.e., for
the total HFB energy calculated for a given Hamiltonian.
, but only in the sum thereof, i.e., for
the total HFB energy calculated for a given Hamiltonian.
As the origin of the pairing interaction is believed to be different
from that of the effective interaction in the particle-hole direction,
it is customary to employ different Hamiltonians
to calculate  and
and  . This, however, leads to
a non-analytical behavior of
. This, however, leads to
a non-analytical behavior of
 due to
the presence of poles in the complex
due to
the presence of poles in the complex  -plane;
hence, to a priori contour-dependent projected HFB energies. We discuss this
question in the next section in the more general context of the DFT
energy functional.
-plane;
hence, to a priori contour-dependent projected HFB energies. We discuss this
question in the next section in the more general context of the DFT
energy functional.



Next: Particle-Number-Projected DFT
Up: Particle-Number-Projected HFB
Previous: Transition matrix elements and
Jacek Dobaczewski
2007-08-08
![]() and
and ![]() . This, however, leads to
a non-analytical behavior of
. This, however, leads to
a non-analytical behavior of
![]() due to
the presence of poles in the complex
due to
the presence of poles in the complex ![]() -plane;
hence, to a priori contour-dependent projected HFB energies. We discuss this
question in the next section in the more general context of the DFT
energy functional.
-plane;
hence, to a priori contour-dependent projected HFB energies. We discuss this
question in the next section in the more general context of the DFT
energy functional.