


Next: Shifted HFB states
Up: Particle-Number Projection and the
Previous: Introduction
Particle-Number-Projected HFB
In the context of HFB
theory [1], the particle-number-projected (PNP) state
is given by the standard expression
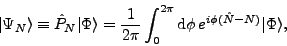 |
(1) |
where  is the PN operator,
is the PN operator,  is the gauge angle,
is the gauge angle,
 is the projection
operator for
is the projection
operator for  particles, and
particles, and
 is the HFB wave function (generalized product state)
which does not have well-defined
particle number. This expression, after the integral
is discretized, is most often used
in practical calculations. However, it only constitutes a specific
realization of a more general form [35] given by the contour integral,
is the HFB wave function (generalized product state)
which does not have well-defined
particle number. This expression, after the integral
is discretized, is most often used
in practical calculations. However, it only constitutes a specific
realization of a more general form [35] given by the contour integral,
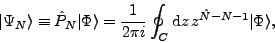 |
(2) |
where C is an arbitrary closed contour encircling the origin  of the complex plane.
of the complex plane.
Subsections
Jacek Dobaczewski
2007-08-08