HFB sum rules

Since the HFB state (11) is a superposition of projected states (13),

$$\vert\Phi\rangle=\sum_{N=0}^{\infty}\vert\Psi_N\rangle ,$$ (18)

the HFB energy $E_{\mbox{\rm\scriptsize {HFB}}}$,

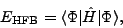$$E_{\mbox{\rm\scriptsize {HFB}}}= \langle\Phi\vert\hat{H}\vert\Phi\rangle ,$$ (19)

can be expressed as the sum of projected energies (15),

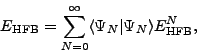$$E_{\mbox{\rm\scriptsize {HFB}}}=\sum_{N=0}^{\infty}\langle\Psi_N\vert\Psi_N\rangle E^N_{\mbox{\rm\scriptsize {HFB}}} ,$$ (20)

weighted by probabilities $\langle\Psi_N\vert\Psi_N\rangle$= $\langle\Phi\vert\Psi_N\rangle$= $\langle\Phi\vert\hat{P}_N\vert\Phi\rangle$ of finding a given PN component in the HFB state. Expression (20) constitutes a useful sum-rule condition, which has to be obeyed by any Hamiltonian-based HFB+PNP approach, and can be used to test the numerical precision of PNP techniques.

A similar sum rule holds for any shifted state

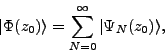$$\vert\Phi(z_0)\rangle=\sum_{N=0}^{\infty}\vert\Psi_N(z_0)\rangle ,$$ (21)

i.e.,

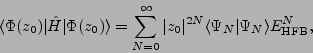$$\langle\Phi(z_0)\vert\hat{H}\vert\Phi(z_0)\rangle =\sum_{N=... ...le\Psi_N\vert\Psi_N\rangle E^N_{\mbox{\rm\scriptsize {HFB}}} ,$$ (22)

where the average energy of the shifted and unnormalized HFB state is related to its HFB energy $E_{\mbox{\rm\scriptsize {HFB}}}(z_0)$ as

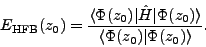$$E_{\mbox{\rm\scriptsize {HFB}}}(z_0)= \frac{\langle\Phi(z_0)... ...t\Phi(z_0)\rangle} {\langle\Phi(z_0)\vert \Phi(z_0)\rangle} .$$ (23)

Finally, the sum rule for the non-diagonal matrix elements can be written as:

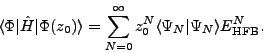$$\langle\Phi\vert\hat{H}\vert\Phi(z_0)\rangle =\sum_{N=0}^{\... ...le\Psi_N\vert\Psi_N\rangle E^N_{\mbox{\rm\scriptsize {HFB}}} .$$ (24)