Figures

  

Figure 1: Neutron OES filter $\Delta_{\mbox{\rm\scriptsize {exp}}}^\nu$ (6) plotted as a function of neutron number N (N-odd). Results for different isotones are marked by dots. The average values of $\Delta_{\mbox{\rm\scriptsize {exp}}}^\nu$ are indicated by gray bars. Experimental data were taken from Ref. [23].

  

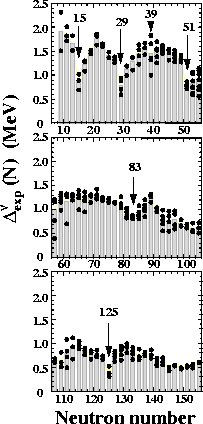Figure 2: Same as in Fig. 1 except for the proton OES filter $\Delta_{\mbox{\rm\scriptsize {exp}}}^\pi$ (6) plotted as a function of Z (Z-odd).

  

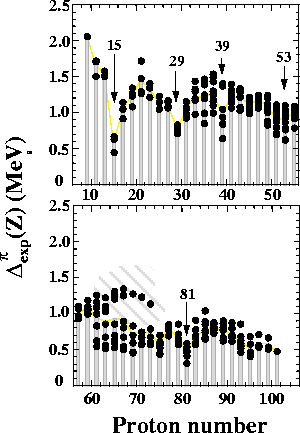Figure 3: Average values of neutron and proton OES filters (6) plotted as functions of the neutron and proton numbers (both N and Z odd), respectively. Experimental masses were taken from Ref. [23].

  

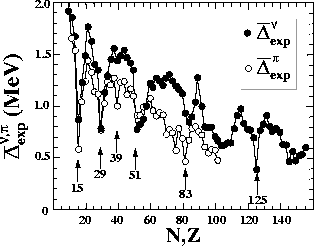Figure 4: Three-mass filters $\Delta^{(3)}_{\mbox{\rm\scriptsize {def}}}$ (1) (thick solid and dotted lines) calculated for the exact binding energies in the deformed-shell-plus-pairing model with $\Omega$=16 for the case of weak (G/d=0.1), intermediate (G/d=0.3), and strong pairing (G/d=0.5). The single-particle spectrum is uniform (e_k=d k), except for the seventh level which is shifted up in energy by d/4 (i.e, e₇=7.25 d). The equivalent gap parameters (56) are shown by thin lines.

  

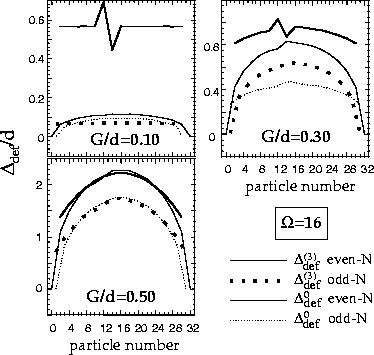Figure 5: Similar to Fig. 4 except for the energy-spacing filters (7) ${\delta{}e}_{\mbox{\rm\scriptsize{def}}}$calculated for G/d=0.1, 0.2, 0.3, and 0.4. The nearly-equidistant single-particle spacings are marked by dots.

  

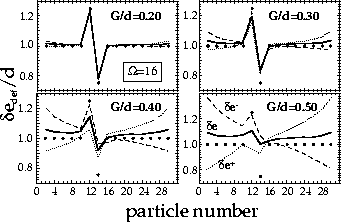Figure 6: Three-mass filters $\Delta^{(3)}_{\mbox{\rm\scriptsize {def}}}$ (1) calculated for the exact (thick lines) and BCS (thin lines) binding energies in the deformed-shell-plus-pairing model with $\Omega$=16 and a nearly-equidistant spectrum. Solid and dotted lines show results for even and odd values of N, respectively.

  

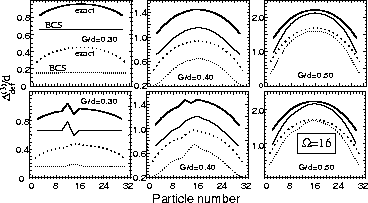Figure 7: Similar to Fig. 6 except for the energy-spacing filters (7) ${\delta{}e}_{\mbox{\rm\scriptsize{def}}}$. The single-particle spacings are marked by dots.

  

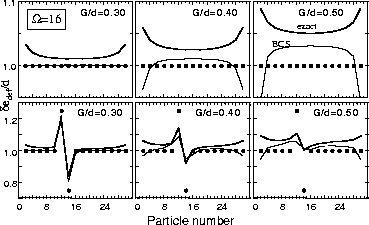Figure 8: Relative error (in percent) of the second-order expressions for the binding energies of the equidistant level model with $\Omega$=16 in the weak (left, G/d$\ll$1; Sec. 3.1.1) and strong (right, d/G$\ll$1; Sec. 3.1.2) pairing limits. In the weak pairing limit, calculations were performed for N=4, 5, 14, and 15. To realize the strong-pairing situation, only large particle numbers, N=14 and 15, were considered in the d/G$\ll$1 case.

  

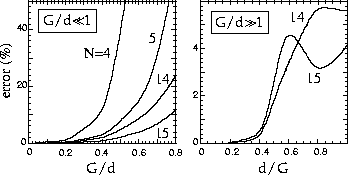Figure 9: Exact binding energies $B_{\mbox{\rm\scriptsize{PPQ}}}$ (solid line) of particles in the j=19/2 single-j shell interacting with the pure QQ interaction (G=0). Energies obtained within the HFB approximation are shown with the dashed line.

  

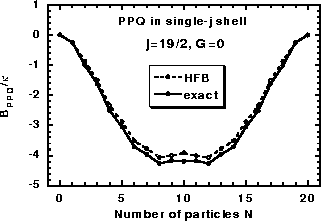Figure 10: Exact values of the three-mass filter $\Delta^{(3)}_{\mbox{\rm\scriptsize {PPQ}}}$within the j=19/2 PPQ calculated for the pairing strengths $G/\kappa$indicated at the right-hand side.

  

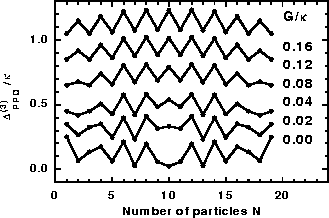Figure 11: Exact values of the OES $\Delta_{\mbox{\rm\scriptsize {PPQ}}}$ (6) (a) and of the energy spacing ${\delta{}e}_{\mbox{\rm\scriptsize {PPQ}}}$ (8) (b) calculated within the j=19/2 PPQ model.

  

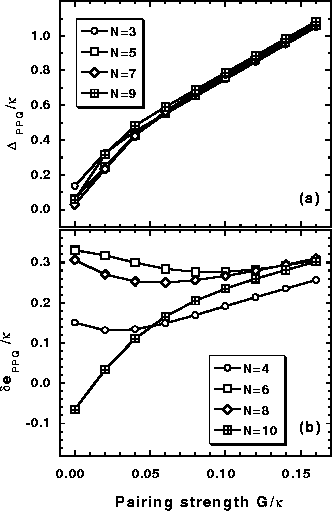Figure 12: Same as in Fig. 11 except for the HFB results.

  

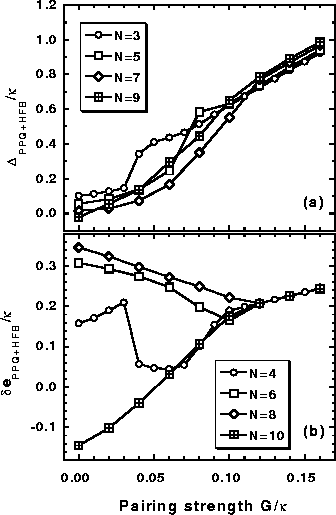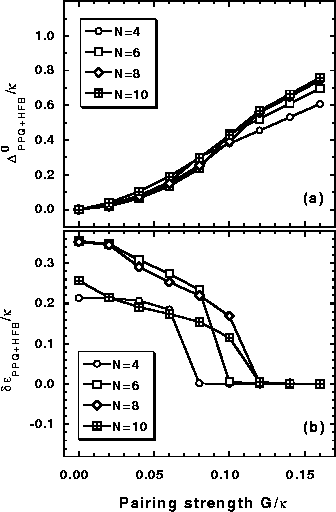
Figure 13: Same as in Fig. 11 except for the $\Delta_{\mbox{\rm\scriptsize{PPQ+HFB}}}^0$ HFB order parameter (56) and the differences of HFB canonical energies $\delta\varepsilon_{\mbox{\rm\scriptsize{PPQ+HFB}}}$ (65).