Two-dimensional rotational and mirror symmetry O $^{z\perp }(2)$

It follows from the S$_z$ invariance of the density matrices (1) and (2) that $\rho (\bm{r},\bm{r}')$ and $\bm{s}_z(\bm{r},\bm{r}')$ do not change signs under S$_z$, while $\bm{s}_{\perp}(\bm{r},\bm{r}')$ does. All scalar functions invariant under S$_z$ depend on $z$, $z'$ only through $z^2=\bm{r}_z\cdot\bm{r}_z$, $z^{\prime 2}=\bm{r}'_z\cdot\bm{r}'_z$, and $zz'=\bm{r}_z\cdot\bm{r}'_z$. For instance, Eq. (31) for the nonlocal scalar density now takes the form

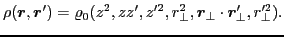$$\rho (\bm{r}, \bm{r}')=\varrho_0(z^2,zz',z'^2,r^2_{\perp},\bm{r}_{\perp}\cdot\bm{r}'_{\perp},r^{\prime 2}_{\perp}).$$ (43)

There exist two pseudoscalars formed from $\bm{r}_z$, $\bm{r}'_z$, $\bm{r}_{\perp}$, $\bm{r}'_{\perp}$, namely $\bm{r}_z\cdot(\bm{r}_{\perp}\times\bm{r}'_{\perp})$ and $\bm{r}'_z\cdot(\bm{r}_{\perp}\times\bm{r}'_{\perp})=(zz'/z^2)\bm{r}_z\cdot(\bm{r}_{\perp}\times\bm{r}'_{\perp})$ equal to each other up to the scalar factor $zz'/z^2$. The square $(\bm{r}_z\cdot(\bm{r}_{\perp}\times\bm{r}'_{\perp}))^2 =z^2(r^2_{\perp}r'^2_{\perp}-(\bm{r}_{\perp}\cdot\bm{r}'_{\perp})^2)$ is, of course, a scalar.

To fulfill the transformation rules, the general forms of Eqs. (32) and (33) of the components of the nonlocal spin density should be modified in the following way:

$$\bm{s}_z(\bm{r}, \bm{r}') = (\bm{r}_z\cdot(\bm{r}_{\perp}\times\bm{r}'_{\perp}))\varrho_z(z^2... ...2,r^2_{\perp},\bm{r}_{\perp}\cdot\bm{r}'_{\perp},r^{\prime 2}_{\perp}) \bm{r}_z$$

$$+(\bm{r}'_z\cdot(\bm{r}_{\perp}\times\bm{r}'_{\perp})) \varrho_z'... ...2,r^2_{\perp},\bm{r}_{\perp}\cdot\bm{r}'_{\perp},r^{\prime 2}_{\perp})\bm{r}'_z$$

$$+\varphi_z(z^2,zz',z'^2,r^2_{\perp},\bm{r}_{\perp}\cdot\bm{r}'_{\perp},r^{\prime 2}_{\perp})(\bm{r}_{\perp}\times\bm{r}'_{\perp}),$$ (44)

and

$$\bm{s}_{\perp}(\bm{r}, \bm{r}') = (\bm{r}_z\cdot(\bm{r}_{\perp}\times\bm{r}'_{\perp})) \varrho_{\pe... ..._{\perp},\bm{r}_{\perp}\cdot\bm{r}'_{\perp},r^{\prime 2}_{\perp})\bm{r}_{\perp}$$

$$+(\bm{r}'_z\cdot(\bm{r}_{\perp}\times\bm{r}'_{\perp})) \varrho_{\... ...{\perp},\bm{r}_{\perp}\cdot\bm{r}'_{\perp},r^{\prime 2}_{\perp})\bm{r}'_{\perp}$$

$$+\varphi_{\perp}(z^2,zz',z'^2,r^2_{\perp},\bm{r}_{\perp}\cdot\bm{r}'_{\perp},r^{\prime 2}_{\perp})(\bm{r}_z\times\bm{r}_{\perp})$$

$$+\varphi_{\perp}'(z^2,zz',z'^2,r^2_{\perp},\bm{r}_{\perp}\cdot\bm{r}'_{\perp},r^{\prime 2}_{\perp})(\bm{r}'_z\times\bm{r}'_{\perp}).$$ (45)

It follows from Eqs. (43), (44), and (45) that the local zero-order densities for $\bm{r}_z =\bm{r}'_z$ and $\bm{r}_{\perp}=\bm{r}'_{\perp}$ can be written in the general form:

$$\rho (\bm{r}) = \rho_0(z^2,r^2_{\perp}),$$ (46)

$$\bm{s}_z(\bm{r}) = 0,$$ (47)

$$\bm{s}_{\perp}(\bm{r}) = \phi_{\perp}(z^2,r^2_{\perp})(\bm{r}_z\times\bm{r}_{\perp}).$$ (48)

The local kinetic density $\tau (\bm{r})$ is of the form (46) too. On the other hand, the pseudoscalar density $J(\bm{r})$ vanishes. The densities $\bm{T}(\bm{r})$ and $\bm{F}(\bm{r})$, are pseudovectors; hence, they take the form (48). On the other hand, vectors $\bm{j}(\bm{r})$ and $\bm{J}(\bm{r})$ are linear combinations of the components of the position vector:

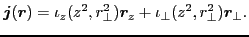$$\bm{j}(\bm{r})=\iota_z(z^2,r^2_{\perp})\bm{r}_z+\iota_{\perp}(z^2,r^2_{\perp})\bm{r}_{\perp}.$$ (49)

The spin-curl $\bm{J}(\bm{r})$ takes a similar form to that of (49). Finally, $\underline{\mathsf{J}}(\bm{r})$ is a pseudotensor. Therefore, as follows from (25), its general form is given by:

$$\underline{\mathsf{J}}(\bm{r}) = \theta_{zz\perp}(z^2,r^2_{\perp})\underline{\bm{r}_z\otimes(\bm{r}_z\times\bm{r}_{\perp})}$$

$$+ \theta_{\perp z\perp}(z^2,r^2_{\perp})\underline{\bm{r}_{\perp}\otimes(\bm{r}_z\times\bm{r}_{\perp})}.$$ (50)