Density matrices and densities

Within the HFB approach to the nuclear many-body problem, the mean value of a many-body Hamiltonian is a functional (the energy functional) of the p-h and p-p density matrices defined, respectively, as

$$\hat{\rho}(\bm{r}st,\bm{r}'s't') = \langle \Psi \vert a_{\bm{r}'s't'}^{+}a_{\bm{r}st}\vert\Psi \rangle ,$$ (1)

$$\hat{\breve{\rho}}(\bm{r}st,\bm{r}'s't') = 4s't'\langle \Psi \vert a_{\bm{r}'-s'-t'}a_{\bm{r}st}\vert\Psi \rangle ,$$ (2)

where $a_{\bm{r}st}^{+}$ and $a_{\bm{r}st}$ create and annihilate, respectively, nucleons at point $\bm{r}$, spin $s$= $\pm\tfrac{1}{2}$, and isospin $t$= $\pm\tfrac{1}{2}$, while $\vert\Psi \rangle$ is the HFB independent-quasiparticle state. The properties of density matrices that directly result from their definitions are the following:

$$\hat{\rho}^{\ast}(\bm{r}st,\bm{r}'s't') = \hat{\rho}(\bm{r}'s't',\bm{r}st),$$ (3)

$$\hat{\breve{\rho}}(\bm{r}st,\bm{r}'s't') = -16ss'tt'\hat{\breve{\rho}}(\bm{r}'-s'-t',\bm{r}-s-t).$$ (4)

The dependence on the spin and isospin variables in the density matrices can be easily separated by expanding in the spin and isospin Pauli matrices $\hat{\bm{\sigma}}_{ss'}$ and $\hat{\tau}^k_{tt'},\ (k=1,\, 2,\, 3)$, respectively:

$$\hat{\rho}(\bm{r}st,\bm{r}'s't') = \tfrac{1}{4}\left(\rho_0(\bm{r},\bm{r}')\delta_{ss'} +\bm{s}_0(\bm{r},\bm{r}')\cdot \hat{\bm{\sigma}}_{ss'}\right)\delta_{tt'}$$

$$+ \tfrac{1}{4}\sum_k\left(\delta_{ss'}{\rho}_k(\bm{r},\bm{r}') + \bm{s}_k(\bm{r},\bm{r}')\cdot \hat{\bm{\sigma}}_{ss'}\right) \hat{\tau}_{tt'}^k,$$ (5)

$$\hat{\breve{\rho}}(\bm{r}st,\bm{r}'s't') = \tfrac{1}{4}\left(\breve{\rho}_0(\bm{r},\bm{r}')\delta_{ss'} + \breve{\bm{s}}_0(\bm{r},\bm{r}')\cdot \hat{\bm{\sigma}}_{ss'}\right)\delta_{tt'}$$

$$+ \tfrac{1}{4}\sum_k\left(\delta_{ss'}\breve{\rho}_k(\bm{r},\bm{r}'... ...\bm{s}}_k(\bm{r},\bm{r}')\cdot\hat{\bm{\sigma}}_{ss'}\right)\hat{\tau}_{tt'}^k,$$ (6)

where $k=0,\ 1,\ 2,\ 3$. The spin-isospin components of the p-h ($\rho_k$, $\bm{s}_k$) and p-p ( $\breve{\rho}_k$, $\breve{\bm{s}}_k$) nonlocal densities are functions of two position vectors $\bm{r}$ and $\bm{r}'$ and have the following symmetry properties that result from Eqs. (3) and (4):

$$\rho_k(\bm{r},\bm{r}') = \rho^{*}_k(\bm{r}',\bm{r}),$$

$$\bm{s}_k(\bm{r},\bm{r}') = \bm{s}^{*}_k(\bm{r}',\bm{r}),$$ (7)

for $k=0,\ 1,\ 2,\ 3$, and:

$$\breve{\rho}_k (\bm{r},\bm{r}') = \mp \breve{\rho}_k (\bm{r}',\bm{r}),$$

$$\breve{\bm{s}}_k (\bm{r},\bm{r}') = \pm \breve{\bm{s}}_k (\bm{r}',\bm{r}),$$ (8)

where the upper sign is for $k=0$ (isoscalars) and the lower for $k=1,2,3$ (isovectors).

In general, the p-h and p-p density matrices transform differently under the single-particle unitary transformations. However, it is proved in I that for the spatial transformations such as rotations, space-inversion, etc., the transformation rules for the p-p density matrix are the same as those for the p-h density matrix. These rules are obviously the same for all the isospin components. Therefore, in further discussion of the space symmetries, we shall omit the accent ``breve" and the index $k$. Also, we shall not take into account conditions (7) and (8), i.e., the hermiticity of the p-h densities and the symmetry or antisymmetry of the p-p densities. We mention only that the former condition ensures the reality of all the p-h local densities, whereas the latter one results in vanishing of either the isoscalar or the isovector p-p local densities.

Within the local density approximation, the energy functional is built from the local densities ( $\bm{r}=\bm{r}'$) and derivatives thereof. The exact definitions of all used local densities are given, e.g., in Refs.[9,10]. Here we only provide schematic definitions that clearly expose the corresponding spatial properties. The densities of interest are:

• zero-order local densities
  • particle or pairing density

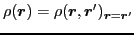    $$\rho (\bm{r})=\rho (\bm{r},\bm{r}')_{\bm{r}=\bm{r}'}$$ (9)

    
    

  • spin density

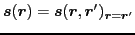    $$\bm{s}(\bm{r})=\bm{s}(\bm{r},\bm{r}')_{\bm{r}=\bm{r}'}$$ (10)

    
    

• first-order local densities
  • current density

    $${\bm{j}}(\bm{r}) =\tfrac{1}{2i}\big[ (\bm{\nabla} - \bm{\nabla}') {\rho}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'}$$ (11)

    
    

  • spin-current density

    $${{\mathsf J}}(\bm{r}) =\tfrac{1}{2i}\big[ (\bm{\nabla} - \bm{\nabla}')\otimes {\bm{s}}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'},$$ (12)

    
    
    which is decomposed into the spin-divergence (trace of $\mathsf{J}$) density $J$, the spin-curl (antisymmetric part of $\mathsf{J}$) density $\bm{J}$, and the traceless symmetric spin-current density¹ $\underline{\mathsf{J}}$:
    

    $$J(\bm{r}) = \tfrac{1}{2i}\big[ (\bm{\nabla} - \bm{\nabla}')\cdot {\bm{s}}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'},$$ (13)

    $${\bm{J}}(\bm{r}) = \tfrac{1}{2i}\big[ (\bm{\nabla} - \bm{\nabla}')\times {\bm{s}}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'},$$ (14)

    $$\underline{{\mathsf J}}(\bm{r}) = \tfrac{1}{2i}\big[ \underline{(\bm{\nabla} - \bm{\nabla}')\otimes {\bm{s}}(\bm{r},\bm{r}')}\big]_{\bm{r}=\bm{r}'}$$ (15)

    
    
• second-order local densities
  • kinetic density

    $${\tau}(\bm{r}) =\big[ (\bm{\nabla}\cdot\bm{\nabla}') {\rho}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'}$$ (16)

    
    

  • spin-kinetic density

    $$\bm{T}(\bm{r}) =\big[ (\bm{\nabla}\cdot\bm{\nabla}') \bm{s}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'}$$ (17)

    
    

  • spin-tensor density

    $${\bm{F}}(\bm{r}) =\tfrac{1}{2}\big[ (\bm{\nabla} \!\otimes\!\bm{\... ...!\otimes\!\bm{\nabla})\!\cdot\! {\bm{s}}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'}.$$ (18)

    
    

We confine ourselves to the second-order derivatives as is usually done. But our analysis can also be extended to higher-order derivatives of the nonlocal densities that have recently been considered.[11]