Nonlocal and local fields

Let $\bm{r}$ and $\bm{r}'$ be two arbitrary, linearly independent position vectors. Then the vector product $\bm{r}\times\bm{r}'$ is the third linearly independent vector, and all three form a basis in the three-dimensional space of positions. The scalar products: $\bm{r}\cdot\bm{r}=r^2$, $\bm{r}'\cdot\bm{r}'=r^{\prime 2}$, and $\bm{r}\cdot\bm{r}'$ form three independent scalars quadratic in $\bm{r}$, $\bm{r}'$. It is impossible to form a cubic scalar because $\bm{r}\cdot (\bm{r}\times\bm{r}')=\bm{0}$ and $\bm{r}'\cdot (\bm{r}\times\bm{r}')=\bm{0}$. Six possible outer products of the three vectors in question form the following second rank Cartesian tensors:

-

three quadratic tensors -- $\bm{r}\otimes\bm{r}$, $\bm{r}'\otimes\bm{r}'$, and $\bm{r}\otimes\bm{r}'$;
the first two tensors are symmetric and their traces are $r^2$ and $r^{\prime 2}$, respectively;
the vector antisymmetric part of the third tensor is $\bm{r}\times\bm{r}'$ and its trace is $\bm{r}\cdot\bm{r}'$.

-

two traceless cubic tensors -- $\bm{r}\otimes(\bm{r}\times\bm{r}')$ and $\bm{r}'\otimes(\bm{r}\times\bm{r}')$ with the vector antisymmetric parts equal to $\bm{r}\times(\bm{r}\times\bm{r}')=(\bm{r}\cdot\bm{r}')\bm{r} -r^2\bm{r}'$ and $\bm{r}'\times(\bm{r}\times\bm{r}')=-(\bm{r}\cdot\bm{r}')\bm{r}' -r^{\prime 2}\bm{r}$, respectively.

-

one fourth-order tensor $(\bm{r}\times\bm{r}')\otimes (\bm{r}\times\bm{r}')$ which can be expressed as a linear combination of the quadratic tensors with scalar coefficients:

$$(\bm{r}\times\bm{r}')\otimes (\bm{r}\times\bm{r}') = (\bm{r}\cdot\bm{r}')(\bm{r}\otimes\bm{r}'+\bm{r}'\otimes\bm{r}) -(\bm{r}\cdot\bm{r}')^2\mathsf{1}$$

$$- r^2(\bm{r}'\otimes\bm{r}')-r^{\prime 2}(\bm{r}\otimes\bm{r})+r^2r^{\prime 2}\mathsf{1},$$ (19)

where $(\mathsf{1})_{ab}=\delta_{ab}$ ( $a,\ b=x,\ y,\ z$) is the unit tensor.

Having listed all the independent scalars, vectors, and tensors that can be constructed from vectors $\bm{r}$ and $\bm{r}'$, we are able to give general expressions for the nonlocal isotropic fields depending on the two position vectors. We note that (i) any scalar field must be an arbitrary function of the independent scalar functions:

$$Q(\bm{r},\bm{r}')=q_0(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2});$$ (20)

(ii) any vector field must be a linear combination of $\bm{r}$, $\bm{r}'$, and $\bm{r}\times\bm{r}'$ with scalar coefficients:

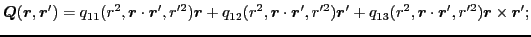$$\bm{Q}(\bm{r},\bm{r}')=q_{11}(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2}... ...ime 2})\bm{r}' +q_{13}(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2})\bm{r}\times\bm{r}';$$ (21)

and (iii) any symmetric traceless tensor field must be a linear combination of the five basic tensors:

$$\underline{\mathsf{Q}}(\bm{r},\bm{r}') = q_{21}(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2})\underline{\bm{r}\otim... ...} +q_{23}(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2})\underline{\bm{r}\otimes\bm{r}'}$$

$$+q_{24}(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2})\underline{\bm{r}\oti... ...\bm{r}\cdot\bm{r}',r^{\prime 2})\underline{\bm{r}'\otimes(\bm{r}\times\bm{r}')}$$

$$= q_{21}(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2})(\bm{r}\otimes\bm{r}-\... ...\bm{r}',r^{\prime 2})(\bm{r}'\otimes\bm{r}'-\tfrac{1}{3}r^{\prime 2}\mathsf{1})$$

$$+q_{23}(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2})[\tfrac{1}{2}(\bm{r}\otimes\bm{r}'+\bm{r}'\otimes\bm{r})-\tfrac{1}{3}(\bm{r}\cdot\bm{r}')\mathsf{1}]$$

$$+q_{24}(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2})\tfrac{1}{2}(\bm{r}\otimes(\bm{r}\times\bm{r}')+(\bm{r}\times\bm{r}')\otimes\bm{r})$$

$$+q_{25}(r^2,\bm{r}\cdot\bm{r}',r^{\prime 2})\tfrac{1}{2}(\bm{r}'\otimes(\bm{r}\times\bm{r}')+(\bm{r}\times\bm{r}')\otimes\bm{r}').$$ (22)

In the expressions above, all $q$'s are arbitrary scalar functions. Scalar fields always have the positive parity. The parities of vector and tensor fields are, in general, indefinite. However, since each independent vector or tensor field does have a definite parity, the vector and tensor fields of definite parities can be easily defined.

It is readily seen from Eqs. (20), (21), and (22) that the corresponding local fields, which depend on one position vector $\bm{r}=\bm{r}'$, only take very simple forms (cf. Appendix A in I):

$$Q(\bm{r}) = q_0(r^2),$$ (23)

$$\bm{Q}(\bm{r}) = q_1(r^2)\bm{r},$$ (24)

$$\underline{\mathsf{Q}}(\bm{r}) = q_2(r^2)(\bm{r}\otimes\bm{r}-\tfrac{1}{3}r^2\mathsf{1}).$$ (25)