Axial symmetry

Let us suppose that rotations and mirror rotations around one axis (say $z$-axis) are SCSs. This symmetry group will be denoted as O $^{z\perp}(2)\subset$O(3). It is the direct product O $^{z\perp}(2)=$S$_z\otimes$SO $^{\perp }(2)$ of the SO $^{\perp }(2)$ group of rotations around the $z$-axis and the two-element group S$_z$ consisting of the reflection in the plane perpendicular to the symmetry axis and the identity. To investigate the axial symmetry, it is convenient to decompose the position vector $\bm{r}$ into the components parallel and perpendicular to the symmetry axis:

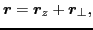$$\bm{r}=\bm{r}_z+\bm{r}_{\perp} ,$$ (29)

which have different transformation properties under the O $^{z\perp }(2)$ transformations. The component $\bm{r}_{\perp}$ is a SO $^{\perp }(2)$ vector whereas $\bm{r}_z$ is not affected by the SO $^{\perp }(2)$ rotations; hence, it is invariant under SO $^{\perp }(2)$. On the other hand, $\bm{r}_z$ changes its sign under the reflection S$_z$, while $\bm{r}_{\perp}$ is S$_z$-invariant.