


Next: FEW-NUCLEON SYSTEMS
Up: Dynamical (Chiral) Symmetry Breaking
Previous: Pion-Pion Lagrangian
Nucleon-Pion Lagrangian
We are now ready to consider another set of composite particles,
the nucleons. We know that there are two nucleons in Nature, of almost
equal mass, the neutron and the proton, so they can be combined into the
iso-spinor
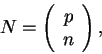 |
(40) |
where  and
and  are the Dirac four-spinors of spin 1/2 particles.
We have already attributed the isospin projections to quarks, Eq. (26), by placing within the quark iso-spinor the quark up
up and the quark down down (sounds logical?). Since the proton is
made of the
are the Dirac four-spinors of spin 1/2 particles.
We have already attributed the isospin projections to quarks, Eq. (26), by placing within the quark iso-spinor the quark up
up and the quark down down (sounds logical?). Since the proton is
made of the  quarks, and the neutron of the
quarks, and the neutron of the  quarks,
their isospin projections are therefore determined as in Eq. (40). In nuclear structure physics one usually uses the opposite
convention, attributing the isospin projection
quarks,
their isospin projections are therefore determined as in Eq. (40). In nuclear structure physics one usually uses the opposite
convention, attributing the isospin projection  =
=
 to a
neutron, in order to make most nuclei to have positive total isospin
projections
to a
neutron, in order to make most nuclei to have positive total isospin
projections 
 0. All this is a matter of convention; one could
as well put the quark up down and the quark down up - the physics
does not depend on that.
0. All this is a matter of convention; one could
as well put the quark up down and the quark down up - the physics
does not depend on that.
Anyhow, the nucleons contain not only the three (valence) quarks, but
also plenty of gluons, and plenty of virtual quark pairs, and we are
unable to find what exactly this state is. Therefore, here we follow the
general strategy of attributing elementary fields to composite
particles. Before we arrive at sufficiently high energies, or small
distances, at which the internal structure of composite objects
becomes apparent, we can safely live without knowing exactly how the
composite objects are constructed.
As usual, having defined elementary fields of particles that we want
to describe, we also have to postulate the corresponding Lagrangian
density. And as usual, we do that by writing a local function of fields
that is invariant with respect to all conserved symmetries. When we
have the nucleon and pion fields at our disposal, and we want to construct
the Lorentz and chiral invariant Lagrangian density, the answer is:
![\begin{displaymath}
{\cal L}_{N\pi}
= - \bar{N}\left(\gamma^\mu\partial_\mu
+ ...
...left[\phi_4+2i\gamma_5\vec{t}\circ \vec{\phi}\right]\right)N .
\end{displaymath}](img165.png) |
(41) |
If you are not tired of this game of guessing the right Lagrangian
densities, you may wonder why the meson fields (within the
square brackets) appear in this particular form. To really see this, we have
to recall more detailed properties of the chiral group
SU(2) SU(2). Its generators
SU(2). Its generators  and
and  in the
spinor representation are given by Eq. (28), however, when
more than one quark is present, we have to use the analogous
generators
in the
spinor representation are given by Eq. (28), however, when
more than one quark is present, we have to use the analogous
generators  and
and  that are sums of
that are sums of  's and
's and
 's for all quarks. In particular, the meson fields
's for all quarks. In particular, the meson fields  belong to the vector representation of SU(2)
belong to the vector representation of SU(2) SU(2). Then,
according to identification (35) and (37), the
first three components
SU(2). Then,
according to identification (35) and (37), the
first three components  form the isovector pion field,
and the fourth component
form the isovector pion field,
and the fourth component  is an isoscalar. This fixes the
transformation properties of
is an isoscalar. This fixes the
transformation properties of  with respect to the
iso-rotations, given by infinitesimal transformation
with respect to the
iso-rotations, given by infinitesimal transformation
 . Since these rotations have identical
form as the real rotations in our three-dimensional space, we do not
show them explicitly. On the other hand, the transformation
properties of
. Since these rotations have identical
form as the real rotations in our three-dimensional space, we do not
show them explicitly. On the other hand, the transformation
properties of  with respect to the chiral rotations, given by
infinitesimal transformation
with respect to the chiral rotations, given by
infinitesimal transformation
 , are
, are
 |
(42) |
There is no magic in this expression - one only has to properly
identify generators of the O(4) group with generators  and
and
 . This is unique, once we fix which components (1,2,3 in our
case) transform under the action of
. This is unique, once we fix which components (1,2,3 in our
case) transform under the action of  . Under the chiral
rotation about the same angle
. Under the chiral
rotation about the same angle
 , the nucleon fields
transform by infinitesimal transformation
, the nucleon fields
transform by infinitesimal transformation
 ,
within the spinor representation of Eq. (28), i.e.,
,
within the spinor representation of Eq. (28), i.e.,
 |
(43) |
It is now a matter of a simple algebra to verify that Lagrangian
density (41) remains invariant under chiral rotations of
fields (42) and (43). Note that the first term in
Eq. (41) is separately chiral invariant, so we could
multiply the second term by an arbitrary constant  .
.
We can now proceed with the transformation to
better variables  and
and  , given by Eq. (35),
which gives,
, given by Eq. (35),
which gives,
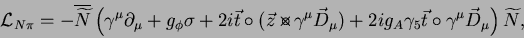 |
(44) |
where
 denotes vector product in the iso-space.
Covariant derivatives of pion fields
denotes vector product in the iso-space.
Covariant derivatives of pion fields  are defined
as in Eq. (39), and the chiral-rotated nucleon field
are defined
as in Eq. (39), and the chiral-rotated nucleon field
 is defined as
is defined as
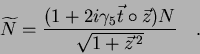 |
(45) |
There are several fantastic results obtained here. First of all,
the nucleon mass term
 appears out of nowhere, and the nucleon mass,
appears out of nowhere, and the nucleon mass,
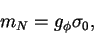 |
(46) |
is given by the chiral-symmetry-breaking value  of the
of the
 field. In principle, we could begin by including the nucleon
mass term already in the initial Lagrangian density (41).
This is not necessary - the nucleon mass results from the same
chiral-symmetry-breaking mechanism that pushes scalar mesons up to
high energies. Second, the third term in Eq. (44) gives
the coupling of nucleons to mesons, and in the potential
approximation it yields the long-distance, low-energy tail of the
nucleon-nucleon interaction, i.e., the one-pion-exchange (OPE) Yukawa
potential Yuk35. Derivation of this potential from
Lagrangian density (44) requires some fluency in the
methods of quantum field theory, so we do not reproduce it here.
Suffice to say, that the OPE potential appears as naturally from
exchanging pions, as the Coulomb potential appears from exchanging
photons via the electron-photon coupling term in Eq. (16).
Last but not least, the last term in Eq. (44) gives the
axial-vector current that defines the weak coupling of nucleons to
electrons and neutrinos. From where phenomena like the
field. In principle, we could begin by including the nucleon
mass term already in the initial Lagrangian density (41).
This is not necessary - the nucleon mass results from the same
chiral-symmetry-breaking mechanism that pushes scalar mesons up to
high energies. Second, the third term in Eq. (44) gives
the coupling of nucleons to mesons, and in the potential
approximation it yields the long-distance, low-energy tail of the
nucleon-nucleon interaction, i.e., the one-pion-exchange (OPE) Yukawa
potential Yuk35. Derivation of this potential from
Lagrangian density (44) requires some fluency in the
methods of quantum field theory, so we do not reproduce it here.
Suffice to say, that the OPE potential appears as naturally from
exchanging pions, as the Coulomb potential appears from exchanging
photons via the electron-photon coupling term in Eq. (16).
Last but not least, the last term in Eq. (44) gives the
axial-vector current that defines the weak coupling of nucleons to
electrons and neutrinos. From where phenomena like the  decay
can be derived. [This term is an independent chiral invariant, so
again we could put a separate coupling constant there; experiment
gives
decay
can be derived. [This term is an independent chiral invariant, so
again we could put a separate coupling constant there; experiment
gives  =1.257(3).]
=1.257(3).]



Next: FEW-NUCLEON SYSTEMS
Up: Dynamical (Chiral) Symmetry Breaking
Previous: Pion-Pion Lagrangian
Jacek Dobaczewski
2003-01-27
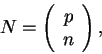
![]() and
and ![]() , given by Eq. (35),
which gives,
, given by Eq. (35),
which gives,
 appears out of nowhere, and the nucleon mass,
appears out of nowhere, and the nucleon mass,