Quantum Electrodynamics (QED)

Classical Jac75 and quantum Itz80 electrodynamics are probably the best established theories of our world. They describe interactions between charged objects, where by the charge we mean the traditional electric charge. Quantum electrodynamics (QED) allows to calculate electrodynamic properties of particles to an unbelievable precision, e.g., the magnetic moment of the electron, calculated up to the eighth order of the perturbation theory Hug99, and the measured value Dyc87,

$$\mu^{\mbox{\scriptsize {th}}}_e = 1.001~159~652~153~5(280)(12)\,{{\textstyle{\frac{e\hbar}{2mc}}}},$$ (14)

$$\mu^{\mbox{\scriptsize {ex}}}_e = 1.001~159~652~188~4(43)\,{{\textstyle{\frac{e\hbar}{2mc}}}},$$ (15)

are in excellent agreement. Moreover, the error of the theoretical value comes mostly from the uncertainty in the measured value of the fine structure constant $\alpha$ (the first error), and less from estimated higher-order effects (the second error).

For an electron coupled to the electromagnetic field, the Lagrangian density, from which everything can be derived, reads

$${\cal L} = -{\textstyle{\frac{1}{4}}}F_{\mu\nu}F^{\mu\nu} -... ...ma^\mu[\partial_\mu+ieA_\mu]\psi_e - m_e \bar{\psi}_e\psi_e .$$ (16)

It is expressed within the relativistic formalism that uses space-time four-coordinates numbered by indices $\mu,\nu$=0,1,2,3. Moreover, we assume that each pair of repeated indices implies summation over them. Here and bellow we use the units defined by $\hbar=c=1$, for which the elementary charge, $e=\sqrt{4\pi\alpha}$, is a dimensionless quantity depending on the fine-structure constant $1/\alpha\simeq137$. (Note that the elementary charge $e$ is positive, while the charge of the electron $q$=$-e$ is negative.) In such a unit system, the only unit left is the energy, so for example, the momentum has the unit of energy, position and time - the unit of (energy)$^{-1}$, and the Lagrangian density $[{\cal{L}}]$=(energy)$^4$ (when ${\cal{L}}$ is integrated over the space-time it gives the dimensionless action $I$).

The first term in the QED Lagrangian density (16) describes the free electromagnetic field defined by the four-potential $A^\mu$$\equiv$ $(\phi,\mbox{{\boldmath {$A$}}})$, containing the standard scalar (Coulomb) potential $\phi$ and vector potential $\mbox{{\boldmath {$A$}}}$. The electromagnetic field tensor $F_{\mu\nu}$ is defined as

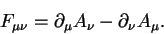$$F_{\mu\nu} = \partial_\mu A_\nu - \partial_\nu A_\mu .$$ (17)

The Euler-Lagrange equations corresponding to this term give the Maxwell equations in free space, i.e., all properties of electromagnetic waves.

The last term in (16) describes the free electron of mass $m_e$ at rest. Its field $\psi_e$ has the structure of the four-component Dirac spinor, but traditionally we do not explicitly show in Lagrangian densities the corresponding indices. The first member of the middle term (the one with $\partial_\mu$) describes the kinetic energy of the electron, and together with the mass term, they constitute the Lagrangian density of a free electron. The corresponding Euler-Lagrange equations give the Dirac equation, i.e., all plane-wave propagation of an electron (and positron) in an otherwise empty space. The kinetic term contains the Dirac 4$\times$4 matrices $\gamma^\mu$ defined by

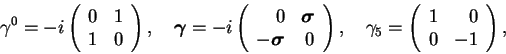$$\gamma^0=-i\left(\begin{array}{rr}0&1\\ 1&0\end{array}\righ... ... \gamma_5=\left(\begin{array}{rr}1&0\\ 0&-1\end{array}\right),$$ (18)

where the standard Pauli 2$\times$2 matrices $\mbox{{\boldmath {$\sigma$}}}$ read

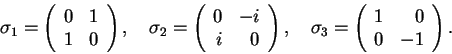$$\sigma_1=\left(\begin{array}{rr}0&1\\ 1&0\end{array}\right)... ... \sigma_3=\left(\begin{array}{rr}1&0\\ 0&-1\end{array}\right).$$ (19)

Finally, the second member of the middle term in (16) describes interaction of the electron with the electromagnetic field. On the one hand, when considered together with the free-electron Lagrangian it gives the Lorentz force that acts on the electromagnetic four-current of the electron,

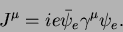$$J^\mu = ie\bar{\psi}_e\gamma^\mu\psi_e .$$ (20)

On the other hand, when considered together with the free-electromagnetic-field Lagrangian, it gives the source terms in the Maxwell equations that correspond to the same electron current $J^\mu$. The structure of the middle term is dictated by the local gauge invariance of the QED Lagrangian density, i.e., invariance with respect to multiplying the electron field by a position-dependent phase. Such a local gauge invariance is at the heart of constructing the Lagrangian densities for all quantum-field theories applicable to the real world. We shall not discuss these aspects during the present course.

Although we only verbally described the role of each term in the QED Lagrangian density (16), derivation and application of the Euler-Lagrange equations is a standard route. However long, painful, and complicated this route might be, it is a well-paved and marked way to get physical answers. In practice, it has already been followed way up, towards incredibly remote summits.