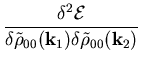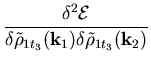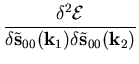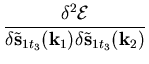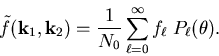Next: Landau Parameters from the
Up: Gamow-Teller strength and the
Previous: Pressure, Incompressibility and Asymmetry
Landau Parameters from the Skyrme energy functional
A simple and instructive description of the residual interaction
in homogeneous INM is given by the Landau interaction developed in the
context of Fermi-liquid theory [50]. Landau parameters
corresponding to the Skyrme forces are discussed in Refs. [21,27,36,37,38,73].
Starting from the full density matrix in (relative) momentum space
 ,
the various densities
are defined as
,
the various densities
are defined as
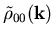 |
= |
 |
(55) |
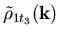 |
= |
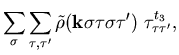 |
(56) |
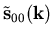 |
= |
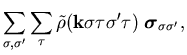 |
(57) |
 |
= |
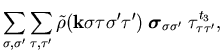 |
(58) |
The kinetic densities are given by
 ,
,
 .
The Landau-Migdal
interaction is defined as
.
The Landau-Migdal
interaction is defined as
The isoscalar-scalar, isovector-scalar, isoscalar-vector, and
isovector-vector channels of the residual interaction are given by
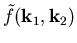 |
= |
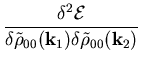 |
(60) |
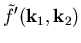 |
= |
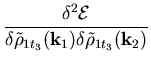 |
(61) |
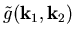 |
= |
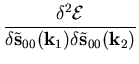 |
(62) |
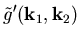 |
= |
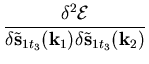 |
(63) |
Assuming that only states at the Fermi surface contribute, i.e.,
 ,
,
 ,
,
 ,
,
 ,
and
,
and  depend on
the angle
depend on
the angle  between
between
 and
and  only, and can be expanded into Legendre
polynomials, e.g.
only, and can be expanded into Legendre
polynomials, e.g.
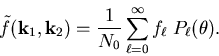 |
(64) |
The normalization factor N0 is the level density at the
Fermi surface
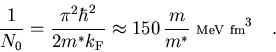 |
(65) |
A variety of definitions of the normalization factor N0 are used
in the literature and great care has to be taken when comparing values
from different groups; see, e.g., Ref.[50] for a detailed
discussion. We use the convention defined in [38].
The Landau parameters corresponding to the general energy
functional (6) are
| f0 |
= |
 |
|
| f0' |
= |
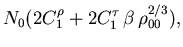 |
|
| g0 |
= |
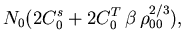 |
|
| g0 |
= |
 |
|
| f1 |
= |
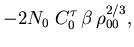 |
|
| f1' |
= |
 |
|
| g1 |
= |
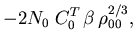 |
|
| g1' |
= |
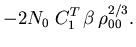 |
(66) |
Higher-order Landau parameters vanish for the second-order
energy functional (12), but not for
finite-range interactions as the Gogny force discussed in
the next Appendix.
The Landau parameters provide a stability criterion for symmetric
unpolarized INM: It becomes unstable for a given interaction
when either  ,
,
 ,
,
 ,
or
,
or  is less
than
is less
than  .
.



Next: Landau Parameters from the
Up: Gamow-Teller strength and the
Previous: Pressure, Incompressibility and Asymmetry
Jacek Dobaczewski
2002-03-15
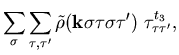
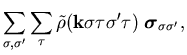
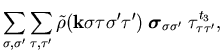
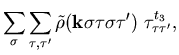
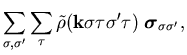
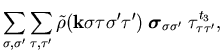
![]() ,
,
![]() .
The Landau-Migdal
interaction is defined as
.
The Landau-Migdal
interaction is defined as