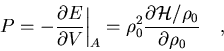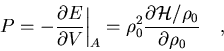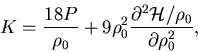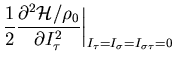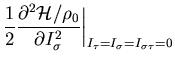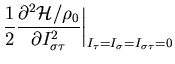Next: Landau Parameters from the
Up: Infinite Nuclear Matter
Previous: ``Equation of state'' of
At the saturation point, all first derivatives of the energy per nucleon
have to vanish and all second derivatives have to be positive. The first
derivative with respect to  is related to the pressure, the second
derivative with respect to
is related to the pressure, the second
derivative with respect to  is related to the incompressibility,
and the second derivatives with respect to the Ii is related to the
asymmetry coefficients. For symmetric matter, the first derivatives with
respect to the Ii vanish because the energy per nucleon is an even
function of all Iis.
The pressure is given by
is related to the incompressibility,
and the second derivatives with respect to the Ii is related to the
asymmetry coefficients. For symmetric matter, the first derivatives with
respect to the Ii vanish because the energy per nucleon is an even
function of all Iis.
The pressure is given by
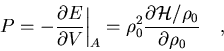 |
(48) |
which gives
The incompressibility is defined as
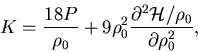 |
(50) |
which, for the Skyrme energy functional (49) at the
saturation point (
 ,
,
 )
gives
)
gives
The asymmetry coefficients are:
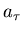 |
= |
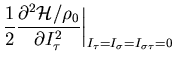 |
|
| |
= |
![$\displaystyle {\textstyle\frac{{1}}{{3}}}
\left[ {\textstyle\frac{{\hbar^2}}{{2...
...3 C_1^{\tau} ) \, \rho_0
\right]
\beta \, \rho_0^{2/3}
+ C_1^{\rho} \, \rho_0 ,$](img328.png) |
(52) |
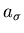 |
= |
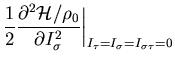 |
|
| |
= |
![$\displaystyle {\textstyle\frac{{1}}{{3}}}
\left[ {\textstyle\frac{{\hbar^2}}{{2...
...{\tau} + 3 C_0^T) \, \rho_0
\right]
\beta \, \rho_0^{2/3}
+ C_0^{s} \, \rho_0 ,$](img331.png) |
(53) |
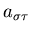 |
= |
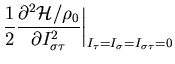 |
|
| |
= |
![$\displaystyle {\textstyle\frac{{1}}{{3}}}
\left[ {\textstyle\frac{{\hbar^2}}{{2...
...\tau} + 3 C_1^T ) \, \rho_0 \right]
\beta \, \rho_0^{2/3}
+ C_1^{s} \, \rho_0 .$](img334.png) |
(54) |
Here,  is the well-known volume asymmetry coefficient of the
liquid-drop model, and
is the well-known volume asymmetry coefficient of the
liquid-drop model, and  and
and
 are its
generalizations to the spin and spin-isospin channels of the interaction.
At the saturation point, all asymmetry coefficients have to be positive.
are its
generalizations to the spin and spin-isospin channels of the interaction.
At the saturation point, all asymmetry coefficients have to be positive.



Next: Landau Parameters from the
Up: Infinite Nuclear Matter
Previous: ``Equation of state'' of
Jacek Dobaczewski
2002-03-15