


Next: Quasiparticle basis
Up: Cranking approximation
Previous: Cranking approximation
To begin with, Eq. (23) can be written explicitly in terms of
the HFB eigenvectors:
| |
|
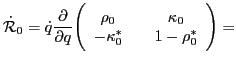 |
(35) |
| |
|
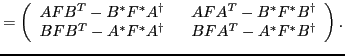 |
|
Evaluating the matrix elements of (35) in the canonical
basis, we obtain
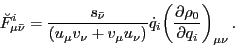 |
(36) |
By differentiating the HFB equation
![$[{\cal W}_0, {\cal R}_0] = 0$](img98.png) with respect to
with respect to  ,
the derivative of the density matrix in (36) can be expressed in
terms of the derivatives of the particle-hole and the pairing mean-fields. The
resulting 2
,
the derivative of the density matrix in (36) can be expressed in
terms of the derivatives of the particle-hole and the pairing mean-fields. The
resulting 2 2 matrix equation is
2 matrix equation is
![\begin{displaymath}
\bigg[ {\cal A}^\dagger
{\dot q_i} \frac {\partial {\cal W}...
... A}, {\cal G} \bigg]
+ \bigg[ {\cal E}_0, {\cal F} \bigg] = 0.
\end{displaymath}](img101.png) |
(37) |
By employing the properties of  and
and  with respect to time
reversal, we obtain
with respect to time
reversal, we obtain
and by approximating the HFB energy matrix in the canonical basis by
its diagonal matrix elements,
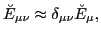 |
|
|
(40) |
one arrives at an approximate ``BCS-equivalent'' expression for the
matrix elements of  in the canonical basis:
in the canonical basis:
![\begin{displaymath}
\breve{F}^{i}_{\mu\nu} \approx \frac{-\dot q_i}{\breve{E}_\m...
...\mu\bar\nu}+\xi^+_{\mu\nu}
(\breve{\Delta}^i)_{\mu\nu}\right],
\end{displaymath}](img107.png) |
(41) |
where
 with
with  ,
,
 , or
, or  . In the following, the results obtained by
using this approximation will be called ATDHFB-C
. In the following, the results obtained by
using this approximation will be called ATDHFB-C .
.
Using relations (40) and (41), the
collective mass tensor (34) can now be expressed in terms of
the derivatives of the mean-field potentials with respect to the
collective coordinates  and BCS-like quasiparticle energies (11),
and BCS-like quasiparticle energies (11),
 |
(42) |
In the one-dimensional case, the resulting expression agrees with
that of Ref. [9].



Next: Quasiparticle basis
Up: Cranking approximation
Previous: Cranking approximation
Jacek Dobaczewski
2010-07-28
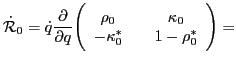
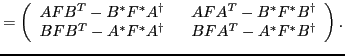
![]() with respect to
with respect to ![]() ,
the derivative of the density matrix in (36) can be expressed in
terms of the derivatives of the particle-hole and the pairing mean-fields. The
resulting 2
,
the derivative of the density matrix in (36) can be expressed in
terms of the derivatives of the particle-hole and the pairing mean-fields. The
resulting 2![]() 2 matrix equation is
2 matrix equation is




![]() and BCS-like quasiparticle energies (11),
and BCS-like quasiparticle energies (11),