Cranking approximation

Next: Canonical basis Up: Approximations to ATDHFB Previous: Approximations to ATDHFB

Cranking approximation

In most of the studies, the time-odd interaction matrix appearing in Eq. (27) is neglected. In the following, this approximation will be referred to as the cranking approximation (ATDHFB-C). In the absence of the term involving , the -matrix can be easily obtained in the quasiparticle basis from the equation:

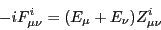$\begin{displaymath} -i F^i_{\mu \nu} = (E_\mu + E_\nu) {Z}^i_{\mu \nu}\,\,\, \end{displaymath}$

(33)

and the collective cranking mass tensor is given by:

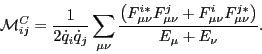$\begin{displaymath} {\cal M}^C_{ij} = \frac {1} {2 {\dot q_i} {\dot q_j}} \sum... ...{i}_{\mu \nu} F^{j\ast}_{\mu \nu} \right) } {E_\mu + E_\nu}. \end{displaymath}$

(34)

It should be noted that Eq. (33) is diagonal in the quasiparticle basis and not in the canonical basis. The essential input to the ATDHFB-C mass tensor (34) is the matrix

. In the following,

is evaluated in both canonical and quasiparticle basis.

Subsections

Jacek Dobaczewski 2010-07-28