Quasiparticle basis

In order to obtain the expression for matrix $F$ in the quasiparticle basis, we invert Eq. (23) and write the matrix expression for ${\cal F}={\cal A}^\dagger {\dot{\cal R}}_0 {\cal A}$

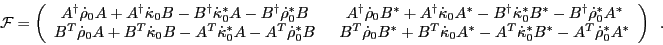$${\cal F} = \left( \begin{array}{cc} A^\dagger {\dot \rho}_0 ... ...\ast - A^T {\dot \rho}_0^\ast A^\ast \end{array}\right)\,\,\,.$$ (43)

Elements (1,1) and (2,2) of ${\cal F}$ vanish because ${\cal R}_0$ is projective, ${\cal R}_0^2={\cal R}_0$. Equating the above expression with Eq. (28), we obtain

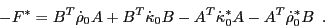$$-F^{\ast} = B^T {\dot \rho}_0 A + B^T {\dot \kappa}_0 B - A^T {\dot \kappa}_0^\ast A - A^T {\dot \rho}_0^\ast B \,\,\,.$$ (44)

In the following, we evaluate the above expression in the simplex basis, as the mean-field analysis has been performed by imposing this symmetry. In this basis, the HFB wave function has the following structure

$$B = \left( \begin{array}{cc} B_+ & 0 \\ 0 & B_- \end{array}... ...( \begin{array}{cc} 0 & A_+\\ A_- & 0 \end{array}\right)\,\,.$$ (45)

The density matrices acquire the following forms in the simplex basis

$$\rho = \left( \begin{array}{cc} B_+^\ast B_+^T & 0 \\ 0 & B_-^\ast B_-^T \end{array}\right) = \left( \begin{array}{cc} \rho_+ & 0\\ 0 & \rho_- \end{array}\right) \,\,\,,$$ (46)

$$\kappa = \left( \begin{array}{cc} 0 & B_+^\ast A_-^T \\ B_-^\ast A_+^T & 0 \end{array}\right) = \left( \begin{array}{cc} 0 & \kappa_+\\ \kappa_- & 0 \end{array}\right)\,\,\,.$$ (47)

The simplex structure of various terms in Eq. (44) is given by

$$B^T {\dot \rho}_0 A = \left( \begin{array}{cc} 0 & B^T_+ {\dot \rho}_{0+} A_+ \\ B^T_-{\dot \rho}_{0-} A_- & 0 \end{array}\right)\,\,\,,$$

$$A^T {\dot \rho}^\ast_0 B = \left( \begin{array}{cc} 0 & A^T_- {\dot \rho}_{0-}^{\ast} B_- \\ A^T_+{\dot \rho}_{0^+}^{\ast} B_+ & 0 \end{array}\right) \,\,\,,$$

$$B^T {\dot \kappa}_0 B = \left( \begin{array}{cc} 0 & B^T_+ {\dot \kappa}_{0+} B_- \\ B^T_-{\dot \kappa}_{0-} B_+ & 0 \end{array}\right) \,\,\,,$$

$$A^T {\dot \kappa}_0^{\ast} A = \left( \begin{array}{cc} 0 & A^T_- {\dot \kappa}_{0-}^\ast A_+ \\ A^T_+{\dot \kappa}_{0+}^{\ast} A_- & 0 \end{array}\right)\,\,\,.$$ (48)

This yields:

$$-F^{\ast} = \left( \begin{array}{cc} 0 & F_+ \\ F_- & 0 \end{array}\right),$$ (49)

where

$$F_+ = B^T_+ {\dot \rho}_ {0+} A_+ - A^T_- {\dot \rho}_ {0-}^{\ast} B_-$$

$$+ B^T_+ {\dot \kappa}_{0+} B_- - A^T_- {\dot \kappa}_{0-}^{\ast} A_+ ,$$ (50)

$$F_- = B^T_- {\dot \rho}_ {0-} A_- - A^T_+ {\dot \rho}_ {0+}^{\ast} B_+$$

$$+ B^T_- {\dot \kappa}_{0-} B_+ - A^T_+ {\dot \kappa}_{0+}^{\ast} A_- .$$ (51)

Since $F$ is antisymmetric, we have obviously $F_+^T=-F_-$, which is fulfilled explicitly provided $\kappa_+^T=-\kappa_-$.