9.2 Przegląd operatorów

W tabeli poniżej przedstawiono operatory języka C++. W prawej kolumnie użyte są oznaczenia:

Operatory podzielone są na 18 grup — każda grupa odpowiada operatorom o tym samym priorytecie. Grupy wymienione są w kolejności od grupy operatorów o priorytecie najwyższym, w dół według malejącego priorytetu. W pierwszej kolumnie zaznaczona jest kolejność wiązania: 'R' – od prawej do lewej, 'L' – od lewej do prawej.

**Tabela:** Operatory w języku C++
L/R	Funkcja	Użycie
Priorytet 17
L	zasięg klasy	klasa::sklad
L	zasięg przestrzeni nazw	pnaz::sklad
L	zasięg globalny	::naz
Priorytet 16
L	wybór składowej	ob.sklad
L	wybór składowej	wsk->sklad
L	wybór elementu przez indeks	wyr[wyr]
L	wywołanie funkcji	wyr(lista_wyr)
L	konstrukcja wartości	typ(lista_wyr)
R	przyrostkowe zmniejszenie	lwar- -
R	przyrostkowe zwiększenie	lwar++
R	statyczna identyfikacja typu	typeid(typ)
R	dynamiczna identyfikacja typu	typeid(wyr)
R	statyczna konwersja	static_cast<typ>(wyr)
R	dynamiczna konwersja	dynamic_cast<typ>(wyr)
R	konwersja wymuszona	reinterpret_cast<typ>(wyr)
R	konwersja uzmienniająca	const_cast<typ>(wyr)
Priorytet 15
R	pobranie rozmiaru obiektu	sizeof wyr
R	pobranie rozmiaru typu	sizeof(typ)
R	pobranie rozmiaru pakietu	sizeof...(naz)
R	przedrostkowe zmniejszenie	- -lwart
R	przedrostkowe zwiększenie	++lwart
R	negacja bitowa	∼wyr
R	negacja logiczna	!wyr
R	minus jednoargumentowy	-wyr
R	plus jednoargumentowy	+wyr
R	wyłuskanie adresu	&lwart
R	dereferencja	*wsk
R	przydział pamięci na obiekt	new typ
R	przydział pamięci na tablicę	new typ[wyr]
R	zwolnienie obiektu	delete wyr
R	zwolnienie tablicy	delete [] wyr
R	rzutowanie (konwersja)	(typ)wyr
R	deklaracja braku wyjątków	noexcept(wyr)
Priorytet 14
L	wskaźnik do składowej klasy	wsk->*sklad_wsk
L	składowa klasy	ob.*sklad_wskwsk
Priorytet 13
L	mnożenie	wyr * wyr
L	dzielenie	wyr / wyr
L	reszta z dzielenia	wyr % wyr
Priorytet 12
L	dodawanie	wyr + wyr
L	odejmowanie	wyr - wyr
Priorytet 11
L	przesunięcie bitowe w lewo	wyr $\ll$ wyr
L	przesunięcie bitowe w prawo	wyr $\gg$ wyr
Priorytet 10
L	mniejsze od	wyr < wyr
L	mniejsze lub równe od	wyr <= wyr
L	większe od	wyr > wyr
L	większe lub równe od	wyr >= wyr
Priorytet 9
L	równe	wyr = = wyr
L	nierówne	wyr ! = wyr
Priorytet 8
L	koniunkcja bitowa	wyr & wyr
Priorytet 7
L	bitowa różnica symetryczna	wyr ^ wyr
Priorytet 6
L	alternatywa bitowa	wyr \| wyr
Priorytet 5
L	koniunkcja (iloczyn) logiczna	wyr && wyr
Priorytet 4
L	alternatywa (suma) logiczna	wyr $\Vert$ wyr
Priorytet 3
R	operator warunkowy	wyr ? wyr : wyr
Priorytet 2
R	przypisanie	lwar = wyr
R	dodawanie z przypisaniem	lwar += wyr
R	odejmowanie z przypisaniem	lwar -= wyr
R	mnożenie z przypisaniem	lwar *= wyr
R	dzielenie z przypisaniem	lwar /= wyr
R	reszta z przypisaniem	lwar %= wyr
R	przesunięcie w lewo z przypisaniem	lwar $\ll$ = wyr
R	przesunięcie w prawo z przypisaniem	lwar $\gg$ = wyr
R	iloczyn bitowy z przypisaniem	lwar &= wyr
R	alternatywa bitowa z przypisaniem	lwar \|= wyr
R	różnica bitowa z przypisaniem	lwar ^= wyr
Priorytet 1
R	zgłoszenie wyjątku	throw wyr
Priorytet 0
L	operator przecinkowy	wyr , wyr

Dyskusję niektórych z tych operatorów, szczególnie tych związanych z klasami, konwersjami, przestrzeniami nazw i obsługą wyjątków, odłożymy do następnych rozdziałów.

9.2.1 Operatory zasięgu

Operatory te (priorytet 17 w tabeli), zapisywane są za pomocą symbolu „czterokropka” (' ::'). Operator zasięgu globalnego już znamy (patrz rozdział o zasięgu i widoczności deklaracji ). Przypomnijmy, że ::x jest nazwą globalnej zmiennej x zadeklarowanej poza wszystkimi funkcjami i klasami. Użycie „czterokropka” jest konieczne tylko wtedy, gdy nazwa (w naszym przypadku x) jest w danym bloku (funkcji) nazwą innej zmiennej, lokalnej, która wobec tego przesłoniła zmienną globalną o tej samej nazwie.

Operatory zasięgu klasy (pozycja pierwsza w tabeli) omówimy w rozdziale o klasach , a przestrzenie nazw w rozdziale o przestrzeniach nazw .

9.2.2 Grupa operatorów o priorytecie 16

Pierwsze dwa (operator „kropka” i „strzałka”, dotyczą struktur i klas, poznamy je w rozdziale o strukturach .

Operator konstrukcji wartości (Typ(lista_wyr)) jest nam nieznany. Ponieważ dotyczy klas, omówimy go w rozdziale o tworzeniu obiektów . Tu tylko wspomnijmy, że w C++ można konstruować obiekty typów prostych (int, double, ...) tak jakby były one obiektami jakiejś klasy. Zatem int(3) kreuje zmienną typu int i inicjuje ją wartością 3 — składnia jest wobec tego taka, jak gdybyśmy tworzyli obiekt klasy int i wysyłali wartość 3 do konstruktora (tak zwanego konstruktora kopiującego).

Przyrostkowe operatory zmniejszenia i zwiększenia (postdekrementacji i postinkrementacji) zmniejszają (zwiększają) wartość swojego argumentu (który wyjątkowo stoi po ich lewej stronie) o jeden. Czynią to jednak po obliczeniu wartości wyrażenia, w skład którego wchodzą. Tak więc po

Argumentem postinkrementacji i postdekrementacji musi zawsze być l-wartość; np.

Warto pamiętać, że wyrażenie ++w nie jest całkowicie równoważne instrukcji w=w+1. Ta druga forma jest normalną instrukcją przypisania, a zatem najpierw zostanie obliczona wartość wyrażenia po prawej stronie, a potem lokalizacja l-wartości po lewej stronie. Zatem jeśli w jest wyrażeniem złożonym (np. zawiera wywołania funkcji), to wyrażenie to będzie obliczane dwukrotnie. Natomiast podczas opracowywania wyrażenia ++w, samo w będzie obliczane jednokrotnie. Rzadko ma to jakieś znaczenie, ale czasem zrozumienie tego może nas ustrzec przed trudno wykrywalnymi błędami.

Operator identyfikacji typu typeid pozwala na uzyskanie identyfikatora typu podczas kompilacji, a więc statycznie, jak również identyfikatora typu obiektu (ogólnie p-wartości) w czasie wykonania programu, a więc dynamicznie (RTTI; run-time type identification). Ten temat omówimy bardziej szczegółowo w rozdziale o RTTI , ale jeden przykład zastosowania tego operatora podany jest poniżej w programie sizes.cpp.

Operatory konwersji (rzutowania) pozwalają na, w miarę bezpieczną, konwersję wartości jednego typu na wartość innego typu. Ponieważ stosowanie konwersji często, choć nie zawsze, świadczy o złej konstrukcji programu i stwarza okazję do użycia błędnych lub zależnych od implementacji konstrukcji programistycznych, nadano tym operatorom celowo tak długą i niewygodną do pisania formę. Konwersje rozpatrzymy w rozdziale im poświęconym .

9.2.3 Grupa operatorów o priorytecie 15

Pierwsze trzy z opertatorów tej grupy dotyczą pobierania rozmiaru za pomocą operatora sizeof. Reultat jest typu size_t (który jest tożsamy z pewnym typem całkowitym bez znaku, np. unsigned long). Operator ten jest jednoargumentowy. Argumentem może być nazwa typu (w nawiasie okrągłym) lub wyrażenie (nawias jest wtedy niekonieczny) albo tak zwany pakiet. Rozpatrzmy przykład:

P56: sizes.cpp Operator sizeof

      1.  #include <iostream>
      2.  #include <typeinfo>
      3.  using namespace std;
      4.  
      5.  typedef int TABINT15[15];                               ➊
      6.  
      7.  void siz(TABINT15 t1, TABINT15& t2) {                   ➋
      8.     cout << "G. t1 w siz: " << sizeof t1 << endl;
      9.     cout << "H. t2 w siz: " << sizeof t2 << endl;
     10.  }
     11.  
     12.  int main() {
     13.     TABINT15 tab1;                                       ➌
     14.     int      tab2[15];                                   ➍
     15.     int     *tab3 = tab2;                                ➎
     16.  
     17.     if (typeid(tab1) == typeid(tab2))
     18.        cout << "A. Typy tab1 i tab2 takie same"     << endl;
     19.     else
     20.        cout << "A. Typy tab1 i tab2 nie takie same" << endl;
     21.  
     22.     if (typeid(tab2) == typeid(tab3))
     23.        cout << "B. Typy tab2 i tab3 takie same"     << endl;
     24.     else
     25.        cout << "B. Typy tab2 i tab3 nie takie same" << endl;
     26.  
     27.     cout << "C. TABINT15: " << sizeof(TABINT15) << endl; ➏
     28.     cout << "D. tab1    : " << sizeof tab1      << endl; ➐
     29.     cout << "E. tab2    : " << sizeof(tab2)     << endl; ➑
     30.     cout << "F. tab3    : " << sizeof tab3      << endl; ➒
     31.     siz(tab2, tab2);
     32.  }

Na początku dołączamy plik nagłówkowy typeinfo, aby mieć dostęp do narzędzi związanych z identyfikacją typów (patrz rozdział o RTTI ).

W linii ➊ wprowadzamy, za pomocą znanej już nam instrukcji typedef, inną nazwę typu „piętnastoelementowa tablica liczb całkowitych” (patrz rozdział o instrukcji typedef ).

Jak widać z linii ➏ i z pierwszej linii wydruku, operator sizeof prawidłowo rozpoznał rozmiar typu TABINT15. Zauważmy też, że nie można tu pominąć nawiasów, bo TABINT15 jest nazwą typu.

W liniach ➌ i ➍ definiujemy tablice tab1 i tab2 na dwa sposoby — za pomocą wprowadzonej nazwy TABINT15 i bezpośrednio. Porównując typy tych zmiennych widzimy, że rzeczywiście są one takie same (linia 'A' wydruku).

W linii ➎ definiujemy zmienną tab3 typu int* i przypisujemy do niej wartość zmiennej tab2. Przypisanie jest prawidłowe, ale nie zapominajmy, że zachodzi przy tym konwersja standardowa: typy tab2 i tab3 nie są takie same, co widzimy z linii 'B' wydruku.

W liniach ➏-➒ drukujemy rozmiary typu TABINT15 i zmiennych tab1, tab2 i tab3. Wszystkie rozmiary, za wyjątkiem tab3, wynoszą 60, co odpowiada tablicy piętnastu czterobajtowych liczb. Natomiast rozmiar tab3 jest 8, gdyż jest to zmienna typu wskaźnikowego, a nie tablicowego.

W ostatniej linii posyłamy tę samą tablicę tab2 poprzez dwa argumenty do funkcji siz. Pierwszy parametr funkcji jest typu TABINT15, więc wydawałoby się, że funkcja „wie”, że argument będzie tablicą. Drukując jednak (linia 'G' wydruku) wewnątrz funkcji rozmiar zmiennej t1, widzimy, że jest to wskaźnik o rozmiarze 8 — jest tak, gdyż przy wysyłaniu tab2 do funkcji przez wartość i tak zmienna została zrzutowana do typu wskaźnikowego (na stosie został położony adres pierwszego elementu tablicy i nic więcej).

Drugi parametr funkcji siz jest zadeklarowany jako referencja. Teraz żadnej konwersji nie ma, bo nie jest w ogóle tworzona żadna zmienna lokalna, której należałoby przypisać wartość argumentu. Wewnątrz funkcji t2 jest teraz inną nazwą dokładnie tej samej zmiennej, która w funkcji main nazywa się tab2. Zatem i informacja o typie jest ta sama i ' sizeof t2' drukuje 60 (linia 'H' wydruku).

Przedrostkowe operatory zmniejszenia i zwiększenia (predekrementacji i preinkrementacji) działają podobnie do przyrostkowych operatorów zmniejszenia i zwiększenia. Są jednak ważne różnice: operatory te zmniejszają (zwiększają) swój argument przed jego użyciem do obliczenia wartości wyrażenia, w skład którego wchodzą. Tak więc po

Operatory negacji: bitowej i logicznej omówimy poniżej razem z innymi operatorami logicznymi i bitowymi.

Operator jednoargumentowy ' +' jest właściwie operatorem identycznościowym, czyli takim, który „nic nie robi” (ang. no-op). Istnieje tylko dla wygody, aby wyrażenia typu ' k = +5' miały sens. Operatory wyłuskania adresu i dereferencji (& i *) były już omówione w rozdziale na temat typów danych .

Operatory new i delete służą do dynamicznego alokowania i zwalniania pamięci: będą omówione w rozdziale o zarządzaniu pamięcią .

Ostatni operator z tej grupy, oznaczany parą nawiasów okrągłych, to operator rzutowania. Jest on operatorem jednoargumentowym: wynikiem działania tego operatora na p-wartość pewnego typu jest odpowiadająca tej wartości p-wartość innego typu — tego wymienionego w nawiasie. Z operatora tego należy korzystać oględnie; w większości przypadków jego zastosowanie świadczy raczej o złym stylu programowania. Czasem jest jednak przydatny. Na przykład w drugiej instrukcji fragmentu

Rzutowanie zawsze działa na p-wartość i w wyniku daje inną p-wartość, ale nigdy l-wartość. W szczególności rzutowanie nie zmienia typu żadnej zmiennej — typu istniejącej zmiennej zmienić się nie da!

Zamiast operatora rzutowania w C++ zaleca się stosowanie bezpieczniejszych operatorów konwersji, wymienionych w tabeli w grupie odpowiadjącej priorytetowi 16. Omówimy je bardziej szczegółowo w rozdziale im poświęconym .

9.2.4 Grupa operatorów o priorytecie 14

Należą do tej grupy dwa operatory wyboru składowej, które omówimy w rozdziałach na temat klas w C++ (rozdział o wskaźnikach na składowe ).

9.2.5 Operatory arytmetyczne

Wymienione w tabeli operatory arytmetyczne mają oczywiste znaczenie i ich działanie jest niemal takie samo jak w większości innych języków. Występują czasem drobne różnice: np. w Javie operator reszty '%' może mieć dowolne agumenty numeryczne, również typu double. W C/C++ operator ten wymaga argumentów typu całkowitego. Pewien kłopot mogą sprawiać wyrażenia z wartościami ujemnymi jako argumentami. Wiemy, że dzielenie liczb typu całkowitego daje w wyniku liczbę całkowitą, czyli ewentualna część ułamkowa jest obcinana. Jeśli wynik jest dodatni, to dokładna wartość ilorazu jest obcinana w dół, czyli w kierunku zera, natomiast jeśli wynik jest ujemny, to obcięcie jest w górę, a więc też w kierunku zera. Dla operatora reszty spełniona jest zawsze zasada

P57: mod.cpp Operator reszty

      1.  #include <iostream>
      2.  using namespace std;
      3.  
      4.  int main() {
      5.      int    i, j;
      6.  
      7.      i = 19; j = 7; cout << " 19 /  7 = " << i/j << endl;
      8.      i =-19; j = 7; cout << "-19 /  7 = " << i/j << endl;
      9.      i = 19; j =-7; cout << " 19 / -7 = " << i/j << endl;
     10.      i =-19; j =-7; cout << "-19 / -7 = " << i/j << endl;
     11.  
     12.      i = 19; j = 7; cout << " 19 %  7 = " << i%j << endl;
     13.      i =-19; j = 7; cout << "-19 %  7 = " << i%j << endl;
     14.      i = 19; j =-7; cout << " 19 % -7 = " << i%j << endl;
     15.      i =-19; j =-7; cout << "-19 % -7 = " << i%j << endl;
     16.  }

9.2.6 Operatory relacyjne i porównania

Operatory relacyjne (' <', ' <=', ' >', ' >=') i porównania (' ==', ' !=') mają oczywistą interpretację. Wyrażenie ' a == b' ma wartość logiczną odpowiadającą na pytanie czy wartość a jest równa wartości b. Wyrażenie ' a != b' ma wartość logiczną odpowiadającą na pytanie czy wartość a jest różna od wartości b. Argumentami mogą być dwa skalary, czyli p-wartości liczbowe, lub (choć nie zawsze) dwa adresy (wartości zmiennych wskaźnikowych lub wynik operacji wyłuskania adresu). Jest to nieco inaczej niż w Javie, gdzie adresy (czy raczej odniesienia) mogły być argumentami wyłącznie operatorów porównania (' ==' i ' !='), ale nie operatorów relacyjnych. W C++ można porównywać adresy za pomocą operatorów relacyjnych pod warunkiem, że są to adresy elementów tej samej tablicy.

Wynikiem operacji jest wartość logiczna true lub false. Jak mówiliśmy (patrz rozdziału o typie logicznym ), wartości logiczne reprezentowane są w zasadzie przez wartości całkowite: wartość 0 jest równoważna false, a dowolna wartość niezerowa true. Obowiązuje to również dla wartości wskaźnikowych: wartość pusta (nullptr) jest interpretowana jako false, a każda inna jako true.

9.2.7 Operatory bitowe

Operatory bitowe wymienione są w tabeli na pozycjach odpowiadających priorytetom 11 (przesunięcia bitowe), 8, 7 i 6. Argumentami muszą być wartości całkowite, wynik też jest typu całkowitego. Obowiązują przy tym normalne reguły konwersji argumentów do typu wspólnego.

Operatory bitowe nie „interesują” się wartościa liczbową argumentów, ale ich reprezentacją bitową. Przypomnijmy, że zwyczajowo numeruje się bity reprezentujące wartości zmiennych, poczynając od zera, od bitu najmniej znaczącego (odpowiadającego współczynnikowi przy zerowej potędze dwójki) do bitu najbardziej znaczącego. Reprezentując graficznie układ bitów, bit zerowy umieszcza się po prawej stronie, a bit najbardziej znaczący po lewej (patrz rozdział o typach całkowitych ).

Rozpatrzmy zatem bardziej szczegółowo działanie poszczególnych operatorów bitowych na wartości liczbowe. Jeden z nich — negacja bitowa — jest jednoargumentowy, pozostałe są dwuargumentowe.

Operator bitowej negacji ('∼'), działając na wartość całkowitą zwraca nową wartość, w której wszystkie bity ulegają odwróceniu: tam, gdzie w argumencie był

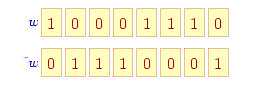
Alternatywa bitowa ('|') jest operatorem dwuargumentowym: dla kolejnych pozycji sprawdzane są pojedyncze bity w obu argumentach i obliczana ich suma logiczna: w wyniku bit na odpowiadającej pozycji jest jedynką (bit ustawiony), jeśli w którymkolwiek argumencie bit na tej pozycji był ustawiony, a zero, gdy w obu argumentach na tej pozycji również występowało zero (jak na rysunku poniżej).

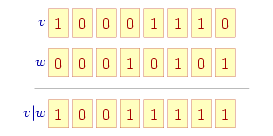
Koniunkcja bitowa ('&') jest też operatorem dwuargumentowym: dla kolejnych pozycji sprawdzane są pojedyncze bity w obu argumentach i obliczany ich iloczyn logiczny: w wyniku bit na odpowiadającej pozycji jest jedynką (bit ustawiony), jeśli w obu argumentach bit na tej pozycji był ustawiony, a zero, gdy w którymkolwiek z argumentów na tej pozycji występowało zero (patrz rysunek).

Jeśli stała określająca tryb nazywa się tryb, to maskowanie jej ze stałą 8 (= 2³) odpowie na pytanie, czy bit in jest czy nie jest ustawiony. Reprezentacja 8 składa się z samych zer, z wyjątkiem pozycji trzeciej (czwarty bit od prawej), na której bit jest ustawiony. Zatem obliczając koniunkcję dostaniemy na wszystkich innych pozycjach na pewno zero, na pozycji czwartej zaś jedynkę, jeśli w tryb ten bit był ustawiony, a zero, jeśli nie był. Zatem wartość wyrażenia tryb & 8 będzie niezerowa wtedy i tylko wtedy, jeśli bit in był w zmiennej tryb ustawiony, niezależnie od stanu innych bitów w tej zmiennej.

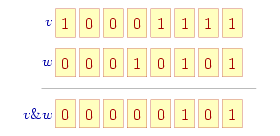
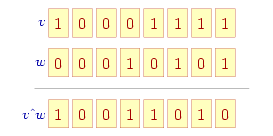
Operator bitowej różnicy symetrycznej ('^') jest też operatorem dwuargumentowym: dla kolejnych pozycji sprawdzane są pojedyncze bity w obu argumentach i obliczana jest ich różnica symetryczna: wynikowy bit na odpowiadającej pozycji jest jedynką (bit ustawiony), jeśli w obu argumentach bity na tej pozycji były różne, a zerem jeśli w obu argumentach na tej pozycji występowały bity takie same — dwa zera albo dwie jedynki.

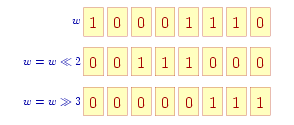
Przesunięcia bitowe ('<<' i '>>') są operatorami dwuargumentowymi: lewy argument jest tu pewną wartością całkowitą na bitach której operacja jest przeprowadzana, prawy argument, również całkowity, określa wielkość przesunięcia. Wyobraźmy sobie, że lewy argument w ma układ bitów jak w górnej części rysunku. Przesunięcie w tej zmiennej bitów w lewo o dwa, 'w = w << 2', odpowiada przesunięciu wszystkich bitów o dwie pozycje w lewo (w kierunku pozycji bardziej znaczących). Bity „wychodzące” z lewej strony są tracone bezpowrotnie. Z prawej strony „wchodzą” bity zerowe. Tak więc po wykonaniu tej instrukcji reprezentacja zmiennej w będzie taka jak w środkowej części rysunku. Analogicznie, po przesunięciu teraz bitów w prawo o trzy pozycje ('w = w >> 3') otrzymamy reprezentację zmiennej w jak w dolnej części rysunku (pod pewnymi warunkami — patrz niżej).

W C/C++ sprawa nie jest taka jasna. Istnieją tu specjalne typy bez znaku (unsigned), za to nie istnieje „potrójny” operator przesunięcia '>>>' w prawo.

Wobec tego w większości implementacji przyjęto następującą konwencję: jeśli typem wartości lewego argumentu jest typ bez znaku (unsigned), to przy przesuwaniu w prawo wchodzą z lewej strony bity zerowe; jeśli natomiast typem wartości lewego argumentu jest typ ze znakiem (signed), to przy przesuwaniu w prawo reprodukowany jest z lewej strony bit znaku, czyli skrajny lewy bit — jeśli było to zero, to zero, jeśli była to jedynka, to jedynka.

Prawy argument operatora przesunięcia, wskazujący na wielkość tego przesunieęcia, zawsze powinien być nieujemny i mniejszy od rozmiaru w bitach wartości, na której dokonujemy przesunięcia. W Javie jest dobrze określone przez specyfikację języka, co się dzieje, jeśli te warunki nie są spełnione; w C/C++ może to zależeć od implementacji i wobec tego lepiej takich konstrukcji unikać.

Na zakończenie rozpatrzmy przykład ilustrujący to, o czym mówiliśmy na temat operacji bitowych.

P58: bits.cpp Operacje na bitach

      1.  #include <iostream>
      2.  using namespace std;
      3.  
      4.  void bitsChar(char k) {
      5.      int bits = 8*sizeof(k);               ➊
      6.      unsigned char mask = 1<<(bits-1);
      7.      for (int i = 0; i < bits; i++) {
      8.          cout << (k & mask ? 1 : 0);
      9.          mask >>= 1;                       ➋
     10.      }
     11.      cout << endl;
     12.  }
     13.  
     14.  void bitsShort(short k) {
     15.      int bits = 8*sizeof(k);
     16.      unsigned short mask = 1<<(bits-1);
     17.      for (int i = 0; i < bits; i++) {
     18.          cout << (k & mask ? 1 : 0);
     19.          mask >>= 1;
     20.      }
     21.      cout << endl;
     22.  }
     23.  
     24.  void bitsInt(int k) {
     25.      int bits = 8*sizeof(k);
     26.      unsigned int mask = 1<<(bits-1);
     27.      for (int i = 0; i < bits; i++) {
     28.          cout << (k & mask ? 1 : 0);
     29.          mask >>= 1;
     30.      }
     31.      cout << endl;
     32.  }
     33.  
     34.  int main() {
     35.      short s = -1; int i = 259;
     36.  
     37.      cout << "char 'a' : "; bitsChar('a');
     38.      cout << "short -1 : "; bitsShort(s);
     39.      cout << "int  259 : "; bitsInt(i);
     40.      cout << endl;
     41.      cout << "ios::in  : "; bitsInt(ios::in);
     42.      cout << "ios::out : "; bitsInt(ios::out);
     43.      cout << "ios::app : "; bitsInt(ios::app);
     44.      cout << "ios::in | ios::out\n           ";
     45.      bitsInt(ios::in | ios::out);
     46.  }

Na początku tego programu definiujemy trzy niemal identyczne funkcje, których zadaniem jest wypisanie bitowej reprezentacji argumentu. Funkcje różnią się tylko typem argumentu: może nim być char, short lub int. W rozdziale o szablonach funkcji dowiemy się, jak można było uniknąć pisania trzech wersji tak podobnych funkcji.

Przyjrzyjmy się jednej z tych funkcji, na przykład funkcji bitsChar. W linii ➊ sprawdzamy, jaki jest rozmiar w bitach wartości argumentu k (tu oczywiście wiemy, że będzie to 8, bo sizeof(k) dla k typu char da jedynkę). Następnie tworzymy maskę mask typu unsigned char. Chodzi nam o to, aby długość maski była taka jak długość k, ale by była to zmienna na pewno bez znaku — w ten sposób przy przesuwaniu w prawo będą z lewej strony „wchodzić” zera. Maskę inicjujemy wartością '1 << 7' (bo bits wynosi 8). Reprezentacja jedynki to siedem bitów zerowych i jeden, prawy (czyli najmłodszy), bit ustawiony. Przesuwając ten układ bitów w lewo otrzymamy liczbę, której reprezentacją jest jedynka i siedem zer (jedynka tym razem z lewej strony). Robimy to po to, by pętla drukująca, która teraz następuje, przebiegała przez kolejne bity liczby k od lewej do prawej, a nie odwrotnie.

Następnie w pętli obliczamy koniunkcję bitową k z maską mask. Ponieważ maska ma tylko jeden bit ustawiony, w ten sposób sprawdzamy, czy odpowiedni bit jest też ustawiony w k. Jeśli tak, to wynikiem koniunkcji będzie jakaś wartość niezerowa, interpretowana jako true w pierwszym argumencie operatora selekcji, a zatem wartością tejże selekcji ' (k&mask ? 1 : 0)' będzie jedynka, która zostanie wypisana na ekranie. Jeśli w k odpowiedni bit nie jest ustawiony, wydrukowane zostanie zero.

W linii ➋ przesuwamy bity w masce o jeden w prawo. Ponieważ zadbaliśmy, aby maska była typu bez znaku, z lewej strony będą wchodzić same zera. Zatem w kolejnych przebiegach pętli maska cały czas będzie zawierać dokładnie jedną jedynkę, „wędrującą” od lewej do prawej. A więc w kolejnych przebiegach pętli sprawdzone i wydrukowane będą, w kolejności od lewej do prawej, wszystkie bity zmiennej k.

Podobnie działają pozostałe dwie funkcje: bitShort i bitInt — jedyna różnica to typ argumentu.

W programie głównym drukujemy reprezentację bitową kilku liczb całkowitych. Wyniki wyglądają następująco:

Dalej ilustrujemy to, co mówiliśmy o stałych ios::in, ios::out itd. Widzimy, że są to pełne potęgi dwójki, a więc w ich reprezentacji bitowej występuje tylko jedna jedynka na odpowiedniej pozycji: w stałej ios::trunc na pozycji czwartej (licząc od zera), a w stałej ios::out na pozycji pierwszej. Obliczając ich alternatywę (sumę) bitową otrzymujemy liczbę, w której reprezentacji bitowej te i tylko te dwa bity są ustawione (ostatnia linia wydruku).

9.2.8 Operatory logiczne

Argumentami operatorów logicznych ' &&' (koniunkcja), ' $\Vert$ ' (alternatywa) i ' !' (negacja) mogą być zarówno wartości typu bool jak i wartości całkowite; w tym ostatnim przypadku wartości zostaną zinterpretowane według normalnej zasady: 0 → false, niezero → true. Obliczona wartość jest typu logicznego: alternatywa (suma logiczna) daje wynik true wtedy i tylko wtedy gdy choć jeden z argumentów ma wartość true, natomiast koniunkcja (iloczyn logiczny) ma wartość true tylko jeśli oba argumenty są true.

Koniunkcja i alternatywa są skrótowe. Oznacza to, że prawy argument nie jest w ogóle obliczany, jeśli po obliczeniu lewego wynik jest już przesądzony. Tak więc

Rozpatrzmy jeszcze jeden przykład ilustrujący skrótowość dwuargumentowych operatorów logicznych:

P59: skrot.cpp Skrótowość operatorów koniunkcji i alternatywy

      1.  #include <iostream>
      2.  using namespace std;
      3.  
      4.  bool fun(int k) {
      5.      k = k - 3;
      6.      cout << "Fun zwraca " << k << endl;
      7.      return k;
      8.  }
      9.  
     10.  int main() {
     11.      if ( fun(1) && fun(2) && fun(3) && fun(4) )      ➊
     12.          cout << "Koniunkcja true"   << endl;
     13.      else
     14.          cout << "Koniunkcja false"  << endl;
     15.  
     16.      if ( fun(1) || fun(2) || fun(3) || fun(4) )      ➋
     17.          cout << "Alternatywa true"  << endl;
     18.      else
     19.          cout << "Alternatywa false" << endl;
     20.  }

W linii ➊ sprawdzany jest warunek w postaci koniunkcji wartości logicznych zwracanych przez funkcję fun (równie dobrze mogłyby to być wartości całkowite). Ponieważ fun(3) zwraca 0 czyli logiczne false, funkcja w ogóle nie zostanie już wywołana z argumentem 4, bo wynik już jest znany: wartością całego wyrażenia w nawiasie musi być false niezależnie od tego, co zwróciłaby funkcja fun dla argumentu 4. Widzimy to z wydruku

9.2.9 Operatory przypisania

W grupie o priorytecie 2 wymienione są operatory zwykłego przypisania (' =') oraz złożone operatory przypisania.

Wykonanie przypisania polega na obliczeniu wartości prawej strony i umieszczeniu wyniku pod adresem l-wartości występującej po stronie lewej. Zauważmy asymetrię: prawa strona mówi co policzyć, lewa gdzie zapisać wynik.

Wartością i typem całego wyrażenia przypisania jest wartość i typ lewej strony po wykonaniu przypisania. Całe przypisanie jest l-wartością. Na przykład

w linii 7 przypisujemy do k wartośc znaku — czyli jego kod ASCII — odczytaną z klawiatury za pomocą metody get wywołanej na rzecz obiektu cin — patrz rozdział o operacjach we/wy . Całe przypisanie ' (k=cin.get())' ma wartość k po przypisaniu; tę wartość porównujemy z predefiniowaną stałą EOF, oznaczającą koniec strumienia danych. Zauważmy, że nawias wokół tego wyrażenia był konieczny, bowiem priorytet porównania, !=, jest wyższy niż priorytet operatora przypisania, a nam chodzi o to, aby najpierw dokonać przypisania, a dopiero jego wynik porównać z EOF. Przykładowe uruchomienie tego programu daje

Złożone operatory przypisania pozwalają na prostszy zapis niektórych przypisań: tych, w których ta sama l-wartość występuje po lewej i prawej stronie przypisania. Zamiast instrukcji

P61: zloz.cpp Przypisania złożone

      1.  #include <iostream>
      2.  using namespace std;
      3.  
      4.  void bitsInt(int k) {
      5.      unsigned int mask = 1<<31;
      6.      for (int i = 0; i < 32; i++, mask >>= 1) {
      7.          cout << (k & mask ? 1 : 0);
      8.          if (i%8 == 7) cout << " ";
      9.      }
     10.      cout << endl;
     11.  }
     12.  
     13.  int main() {
     14.      unsigned int k = 255<<24 | 153<<16 | 255<<8 | 255; ➊
     15.      cout << "k przed: "; bitsInt(k);
     16.      (k <<= 8) >>= 24;                                  ➋
     17.      cout << "k    po: "; bitsInt(k);
     18.  }

Funkcja bitsInt jest tu podobna do tej z programu bits.cpp — tak samo służy do drukowania bitowej reprezentacji liczby całkowitej. W tej wersji z góry założyliśmy, że typ int jest czterobajtowy. Prócz tego przesuwanie maski przenieśliśmy do części inkrementującej nagłówka pętli, umieszczając tam dwie instrukcje wyrażeniowe oddzielone przecinkiem (o operatorze przecinkowym — w jednym z następnych podrozdziałów ). Dodaliśmy też drukowanie spacji po każdej grupie ośmiu bitów, aby uczynić wydruk bardziej przejrzystym.

W linii ➊ konstruujemy liczbę o z góry zadanej reprezenatcji bitowej. Wyrażenie '255 << 24' daje liczbę z samymi jedynkami w najstarszym bajcie (255 to osiem jedynek, następnie przesunięte o 24 pozycje w lewo). Wyrażenie '153 << 16' to układ bajtów 10011001 przesunięty w lewo o 16 pozycji, czyli do bajtu trzeciego od lewej. Z kolei '255 << 8' daje osiem jedynek w bajcie drugim, a samo 255 — osiem jedynek w bajcie najmłodszym. Suma (alternatywa) bitowa „składa” wszystkie te bajty: otrzymujemy zatem liczbę o reprezentacji przedstawionej w pierwszej linii wydruku:

9.2.10 Operator warunkowy

Operator warunkowy (selekcji) jest jedynym operatorem trzyargumentowym. Jego składnia:

Klasyczny przykład zastosowania operatora selekcji to implementacja funkcji max zwracającej większą z wartości swych argumentów:

Inny przykład zastosowania operatora selekcji podany zostanie w następnym podrozdziale.

9.2.11 Operator zgłoszenia wyjątku

Jako przedostatni w tabeli występuje operator zgłoszenia wyjątku throw: omówimy go w rozdziale o wyjątkach .

9.2.12 Operator przecinkowy

Operator przecinkowy jest dwuargumentowy: po dwóch stronach przecinka dwa wyrażenia

Operator przecinkowy jest tu użyty w linii ➊ w warunku pętli while. Mamy tu pierwsze wyrażenie, 'cin >> k', wczytujące kolejną daną z klawiatury, i drugie, po prostu k, dzięki któremu pętla skończy się, gdy wczytana zostanie liczba 0 (gdyż wartością całego wyrażenia przecinkowego jest wartość prawego argumentu). W pętli do r dodawana jest (operator złożonego przypisania) wartość nieco skomplikowanego wyrażenia. Jest to operator selekcji — patrz podrozdział o operatorze selekcji — sprawdzający znak k; w każdym przypadku rezultat będzie znów wartością wyrażenia przecinkowego. Dla k dodatnich będzie to wartość

9.2.13 Alternatywne nazwy operatorów

Forma tekstowa może być zamiennie stosowana z formą wyrażoną za pomocą symboli nieliterowych.

klasa: nazwa klasy	ob: obiekt klasy
sklad: składowa klasy lub przestrzeni nazw	wsk: wskaźnik
wyr: wyrażenie	lwar: l-wartość
pnaz: nazwa przestrzeni nazw	typ: nazwa typu
naz: nazwa

b	m	b $\hat{{\ }}$ m	(b $\hat{{\ }}$ m) $\hat{{\ }}$ m
1	1	0	1
1	0	1	1
0	1	1	0
0	0	0	0

tekstowa	symboliczna	tekstowa	symboliczna
and	&&	and_eq	&=
bitand	&	bitor	\|
compl	∼	not	!
not_eq	!=	or	$\Vert$
or_eq	\|=	xor	^
xor_eq	^=