Wstecz: 13. C-struktury i unie W górę: 13. C-struktury i unie Dalej: 13.2 Unie

---

13.1 C-struktury

Struktura definiuje nowy typ danych. Jest to typ złożony: pojedyncza zmienna typu strukturalnego może zawierać wiele danych (liczb, napisów, wskaźników, itd.). W odróżnieniu od tablic, dane te nie muszą być tego samego typu (jak elementy tablicy).

Definicja C-struktury może mieć następującą postać:

       struct Nazwa {
           Typ1 sklad1;
           Typ2 sklad2;
           ...
       };

Średnik na końcu, po nawiasie zamykającym, jest konieczny!

W C++ po takiej samej definicji nazwą typu jest po prostu Nazwa. Natomiast w C nazwą tego typu jest struct Nazwa — konieczne jest zatem powtórzenie słowa kluczowego struct przy późniejszym użyciu nazwy tego typu. Można tego uniknąć stosując standardową „sztuczkę” ze specyfikatorem typedef:

       typedef struct Nazwa {
           // definicja struktury
       } Nazwa;

Kiedy już zdefiniowaliśmy typ, możemy definiować zmienne tego typu; składnia jest dokładnie taka sama jak składnia deklaracji/definicji zmiennych typów wbudowanych (jak double czy int):

       struct Nazwa a, b;  /* C i C++ */
       Nazwa c, d;         // tylko C++

       struct Nazwa {
           Typ1 skladowa1;
           Typ2 skladowa2;
       } a, b, c, d;

       struct {
           Typ1 skladowa1;
           Typ2 skladowa2;
       } a, b;

Każdy pojedynczy obiekt typu zdefiniowanego jako C-struktura zawiera tyle składowych i takich typów, jak to zostało określone w definicji tej C-struktury. Jeśli zdefiniowany (utworzony) jest obiekt, to do jego składowych odnosimy się za pomocą operatora wyboru składowej. Operator ten ma dwie formy (patrz pozycje 4 i 5 w tabeli operatorów), w zależności od tego, czy odnosimy się do obiektu poprzez jego nazwę, czy poprzez nazwę wskaźnika do niego. Jeśli a jest nazwą obiektu, to do jego składowej o nazwie sklad odnosimy się za pomocą operatora „kropki”:

       a.sklad

       pa->sklad

Ta sama zasada dotyczy nie tylko struktur, które mają postać C-struktur, ale wszystkich struktur i klas w C++.

Zauważmy, że forma pa->sklad jest w zasadzie notacyjnym skrótem zapisu (*pa).sklad, gdyż *pa jest właśnie l-wartością obiektu wskazywanego przez pa. Zatem jeśli a jest identyfikatorem obiektu struktury posiadającej pole x typu double, a pa wskaźnikiem do tego obiektu, to następujące instrukcje są równoważne:

      1.      a.x     = 3.14;
      2.      (&a)->x = 3.14;
      3.      pa->x   = 3.14;
      4.      (*pa).x = 3.14;

Zapamiętajmy zatem:

Tworząc obiekt typu C-struktury można go od razu zainicjować. Składnia jest podobna do tej, jakiej używamy do inicjowania tablicy:

       Nazwa ob = {wyr_1, wyr_2};

W poniższym przykładzie definiujemy strukturę Sam (➊) opisującą, w bardzo uproszczony sposób, samochody. Ma ona dwa pola: predk i  roczn typu, odpowiednio, double i  int. Dwie zmienne typu Sam od razu definiujemy: zmienną skoda i zmienną fiat. Tę drugą również inicjujemy podając w nawiasach klamrowych wartości inicjatorów w kolejności odpowiadającej kolejności pól w definicji struktury Sam. Zmienna skoda jest utworzona, ale nie została zainicjowana, więc wartości jej składowych są na razie nieokreślone. Obie zmienne są globalne.

      1.  #include <iostream>
      2.  using namespace std;
      3.  
      4.  struct Sam {                                ➊
      5.      double predk;
      6.      int    roczn;
      7.  } skoda, fiat{100, 1998};
      8.  
      9.  void pr(const char*,const Sam*);
     10.  
     11.  int main() {
     12.      Sam toyota, *mojsam = &toyota, *vw;     ➋
     13.  
     14.      cout << "Obiekty \'Sam\' maja rozmiar " ➌
     15.           << sizeof(Sam) << " bajtow\n";
     16.      skoda.predk =  120;                     ➍
     17.      skoda.roczn = 1995;
     18.  
     19.      toyota.roczn  = 2012;                   ➎
     20.      mojsam->predk =  180;
     21.  
     22.      vw = new Sam{175,2003};                 ➏
     23.  
     24.      pr("Skoda ",&skoda);
     25.      pr("Fiat  ",&fiat);
     26.      pr("Toyota",&toyota);
     27.      pr("mojsam", mojsam);
     28.      pr("VW    ", vw);
     29.  
     30.      delete vw;
     31.  }
     32.  
     33.  void pr(const char *nazwa, const Sam *sam) {
     34.      cout << nazwa << ": predkosc " << sam->predk
     35.           << ", rocznik " << sam->roczn << endl;
     36.  }

Wewnątrz funkcji main definiujemy jeszcze jeden obiekt typu Sam o nazwie toyota. Prócz tego definiujemy dwie zmienne wskaźnikowe: mojsam zainicjowaną adresem obiektu toyota oraz vw, która na razie nie jest zainicjowana (linia ➋).

W linii ➌ drukujemy rozmiar obiektów typu Sam. Może to być 12 bajtów: 8 bajtów na składową predk typu double i 4 bajty na składową roczn typu int. Na wielu platformach preferowane są rozmiary będące wielokrotnością 8 bajtów; wtedy każdy obiekt będzie zawierał dodatkowe, nieużywane bajty, tzw. padding (wypełnienie). Na komputerze autora ten właśnie przypadek ma miejsce, o czym przekonuje nas wydruk:

    Obiekty 'Sam' maja rozmiar 16 bajtow
    Skoda : predkosc 120, rocznik 1995
    Fiat  : predkosc 100, rocznik 1998
    Toyota: predkosc 180, rocznik 2012
    mojsam: predkosc 180, rocznik 2012
    VW    : predkosc 175, rocznik 2003

W liniach ➎ i następnej wpisujemy wartości do składowych obiektu toyota. W linii ➎ odnosimy się do tego obiektu poprzez jego nazwę, więc używamy notacji z kropką; w linii następnej do tego samego obiektu (patrz linia ➋) odnosimy się poprzez wskaźnik mojsam, zatem używamy notacji ze „strzałką”.

W linii ➏ alokujemy na stercie (poprzez new) nowy obiekt typu Sam i zwrócony adres wpisujemy do wskaźnika vw. Obiekt jest od razu inicjowany poprzez użycie składni z listą inicjatorów w nawiasach klamrowych; jest to dozwolone w nowym standardzie C++11 (zauważmy jednak, że użycie tu znaku równości przed otwierającą klamrą byłoby błędem).

Następnie drukujemy informacje o naszych zmiennych za pomocą funkcji pr. Funkcja ta ma drugi parametr typu wskaźnikowego const Sam*, a więc trzeba do niej wysłać adres obiektu; dlatego jako argument wpisujemy albo zmienną wskaźnikową (bo jej wartością jest właśnie adres), albo, jeśli używamy nazwy obiektu, wyłuskujemy jego adres za pomocą operatora ' &'.

C-struktury są bardzo często używane w funkcjach bibliotecznych. Na przykład, włączając plik nagłówkowy sys/timeb.h mamy do dyspozycji funkcję ftime (funkcje udostępniane przez nagłówek sys/timeb.h nie należą do standardu, ale są zaimplementowane w Linuksie, w wersji C++ firmy Microsoft i w większości innych implementacji tego języka). Funkcja ftime wymaga argumentu w postaci adresu obiektu struktury timeb zdefiniowanej następująco (ta definicja jest już widoczna po włączeniu pliku nagłówkowego sys/timeb.h):

       struct timeb {
           time_t         time;
           unsigned short millitm;
           short          timezone;
           short          dstflag;
       };

2³¹ -1 = 2147483647 2.1⋅10⁹

      1.  #include <iostream>
      2.  #include <cmath>         // sin, cos
      3.  #include <sys/timeb.h>   // ftime
      4.  using namespace std;
      5.  
      6.  int main() {
      7.      timeb start, teraz;                              ➊
      8.      double res = 0;
      9.  
     10.      ftime(&start);                                   ➋
     11.  
     12.      for (int i = 0; i <= 90000000; ++i) {
     13.          if (i%10000000 == 0) {
     14.              ftime(&teraz);                           ➌
     15.              time_t sec = teraz.time - start.time;
     16.              int msec = teraz.millitm;
     17.              msec -=  start.millitm;
     18.              if (msec < 0) {
     19.                  --sec;
     20.                  msec += 1000;
     21.              }
     22.              cout << "Po " << i << " iteracjach: "
     23.                   << sec << "s and " << msec << "ms\n";
     24.          }
     25.          res = cos(res+sin(i));
     26.      }
     27.      cout << "Bezuzyteczny wynik: " << res << endl;
     28.  }

W linii ➊ tworzymy dwie zmienne typu timeb: zmienną start i  teraz. W linii ➋ pierwszą z nich wypełniamy aktualnymi danymi wywołując funkcję ftime, a następnie z drugą z nich robimy to samo w pętli (➌), co 10 milionów obrotów, za każdym razem obliczając czas, jaki upłynął do tego momentu od chwili uruchomienia programu:

    Po 0 iteracjach: 0s and 0ms
    Po 10000000 iteracjach: 0s and 886ms
    Po 20000000 iteracjach: 1s and 769ms
    Po 30000000 iteracjach: 2s and 663ms
    Po 40000000 iteracjach: 3s and 555ms
    Po 50000000 iteracjach: 4s and 438ms
    Po 60000000 iteracjach: 5s and 321ms
    Po 70000000 iteracjach: 6s and 205ms
    Po 80000000 iteracjach: 7s and 90ms
    Po 90000000 iteracjach: 7s and 974ms
    Bezuzyteczny wynik: 0.953078

Nic nie stoi na przeszkodzie, aby składowymi struktury były obiekty innej struktury. Oczywiście, składowymi struktury nie mogą być obiekty tej samej struktury, bo one też musiałyby zawierać obiekty tej struktury, które z kolei też musiałyby zawierać ... i tak ad infinitum...

Wyobraźmy sobie, że chcemy opisywać punkty na płaszczyźnie. Naturalną reprezentacją takich obiektów byłaby struktura o dwóch polach odpowiadających współrzędnym kartezjańskim punktu

       struct Punkt {
           double x, y;
       };

       struct Trojkat {
           Punkt A, B, C;
       };

      1.  #include <iostream>
      2.  #include <cmath>     // sin, cos
      3.  using namespace std;
      4.  
      5.  struct Punkt {
      6.      double x, y;
      7.  };
      8.  
      9.  struct Trojkat {
     10.      Punkt A, B, C;
     11.  };
     12.  
     13.  void info(const Punkt*);               ➊
     14.  void info(const Trojkat*);             ➋
     15.  void rot(Punkt*,double);               ➌
     16.  void rot(Trojkat*,double);             ➍
     17.  
     18.  int main() {
     19.      Punkt A;
     20.      A.x = -1;
     21.      A.y =  2;
     22.  
     23.      Punkt B = { -1, 1 };
     24.  
     25.      Punkt C = { 2 };
     26.      C.y = -1;
     27.  
     28.      Trojkat T = { A, B };
     29.      T.C = C;
     30.  
     31.      cout << "Wyjsciowe punty: ";
     32.      info(&A); info(&B); info(&C);
     33.      cout << "\nTrojkat: ";
     34.      info(&T);
     35.      cout << endl;
     36.  
     37.      rot(&A,90); rot(&B,90); rot(&C,90);                ➎
     38.      cout << "A, B, C po obrocie o 90 stopni:\n    ";
     39.      info(&A); info(&B); info(&C);
     40.      cout << endl;
     41.  
     42.      rot(&T,90); rot(&T,90);                            ➏
     43.      cout << "T po obrocie dwa razy o 90 stopni:\n    ";
     44.      info(&T);
     45.  
     46.      rot(&T,180);                                       ➐
     47.      cout << "T po obrocie o nastepne 180 stopni:\n    ";
     48.      info(&T);
     49.  }
     50.  
     51.  void info(const Punkt* pP) {
     52.      cout << "(" << pP->x << ", " << pP->y << ") ";
     53.  }
     54.  
     55.  void info(const Trojkat* pT) {
     56.      cout << "A="; info(&pT->A);                        ➑
     57.      cout << "B="; info(&pT->B);
     58.      cout << "C="; info(&pT->C);
     59.      cout << endl;
     60.  }
     61.  
     62.  void rot(Punkt* pP, double phi) {
     63.      static double conver = atan(1.)/45;
     64.      phi = phi*conver; // stopnie -> radiany
     65.  
     66.      double c = pP->x;
     67.      pP->x = pP->x * cos(phi) - pP->y * sin(phi);
     68.      pP->y =     c * sin(phi) + pP->y * cos(phi);
     69.  }
     70.  
     71.  void rot(Trojkat* pT, double phi) {
     72.      rot( &pT->A, phi);                                 ➒
     73.      rot( &pT->B, phi);
     74.      rot( &pT->C, phi);
     75.  }

Funkcja ta pobiera adres punktu, dzięki czemu może pracować na oryginale poprzez wskaźnik (dlatego w jej definicji używamy „strzałek” a nie kropek). Jako przykład wybierzmy punkty A = (- 1, 2), B = (- 1, 1), C = (2, - 1), jak po lewej stronie rysunku:

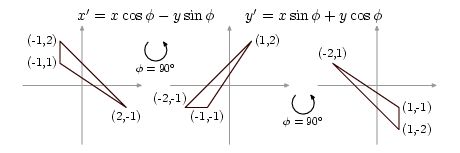
Następnie definiujemy trójkąt o wierzchołkach w punktach opisanych zmiennymi A,  B i  C. Zauważmy, że przypisanie wartości tych obiektów składowym obiektu T powoduje kopiowanie tych wartości. Po zainicjowaniu obiekt T jest niezależny od obiektów A, B i  C. Drukując informację o punktach i trójkącier widzimy, że odpowiada ona sytuacji po lewej stronie rysunku.

Następnie, w linii ➎, dla każdego z punktów wywołujemy funkcję rot, która oblicza ich nowe współrzędne po obrocie o  90^o; ponieważ funkcja pracuje na oryginale, stare współrzędne są zamazywane. Punkty zatem uległy zmianie — ich współrzędne odpowiadają teraz sytuacji ze środkowej części rysunku. Zauważmy, że sam trójkąt T nie zmienił się; jego składowe są bowiem kopiami oryginalnych punktów sprzed zmiany.

    Wyjsciowe punty: (-1, 2) (-1, 1) (2, -1)
    Trojkat: A=(-1, 2) B=(-1, 1) C=(2, -1)

    A, B, C po obrocie o 90 stopni:
        (-2, -1) (-1, -1) (1, 2)
    T po obrocie dwa razy o 90 stopni:
        A=(1, -2) B=(1, -1) C=(-2, 1)
    T po obrocie o nastepne 180 stopni:
        A=(-1, 2) B=(-1, 1) C=(2, -1)

Po dwukrotnym obrocie o kąt 90^o, czyli w sumie o kąt 180^o, trójkąt powinien być (i jest, jak widać z wydruku) ulokowany jak w prawej części rysunku. Po kolejnym obrocie o  180^o (➐) trójkąt wraca do pozycji wyjściowej przedstawionej po lewej stronie rysunku i w ostatniej linii wydruku.

Jak wspomnieliśmy, składową struktury lub klasy nie może z oczywistych względów być obiekt tejże klasy. Nic jednak nie stoi na przeszkodzie, aby taką składową był wskaźnik do obiektu tej struktury/klasy. Jest to przypadek bardzo często spotykany i użyteczny, ponieważ umożliwia tworzenie list obiektów. W każdym obiekcie struktury zawarta jest wtedy składowa będąca adresem następnego obiektu na liście. Mówimy wtedy o liście jednokierunkowej — stosuje się też listy dwukierunkowe, w których każdy obiekt „pamięta” adres zarówno swego następnika, jak i poprzednika.

Zobaczmy, jak można taką prostą listę utworzyć. Konstruujemy strukturę Wezel zawierającą pewną liczbę pól z jakąś informacją; w przykładzie poniżej są to dwie liczby typu double — polom tym nadajemy nazwy szer i wyso. Prócz tego definiujemy dodatkowe pole next typu Wezel*. Składowe obiektów odpowiadające temu polu będą właśnie zawierać adresy obiektów następnych na liście. Umawiamy się, że element ostatni, który już następnika nie ma, ma w tej składowej wskaźnik pusty nullptr (odpowiadający NULL). Inna często spotykana konwencja polega na tym, że element ostatni zawiera wskaźnik wskazujący na samego siebie lub na element pierwszy — w tym ostatnim przypadku otrzymujemy listę cykliczną.

      1.  #include <iostream>
      2.  using namespace std;
      3.  
      4.  struct Wezel {
      5.      double szer;
      6.      double wyso;
      7.      Wezel *next;
      8.  };
      9.  
     10.  void wstaw_dane(Wezel* n, double s, double w, Wezel* next);
     11.  void drukuj_liste(const Wezel* n);
     12.  void drukuj_liste_odwrotnie(const Wezel* n);
     13.  
     14.  int main() {
     15.      Wezel A = {4, 44, nullptr};        ➊
     16.      Wezel B, D, *head;
     17.  
     18.      Wezel* pC = new Wezel;             ➋
     19.  
     20.      wstaw_dane(&B,3,33,&A);
     21.      wstaw_dane(pC,2,22,&B);
     22.      wstaw_dane(&D,1,11,pC);
     23.  
     24.      head = &D;                         ➌
     25.  
     26.      drukuj_liste(head);
     27.      drukuj_liste_odwrotnie(head);
     28.  
     29.      delete pC;
     30.  }
     31.  
     32.  void wstaw_dane(Wezel* n, double s, double w, Wezel* next) {
     33.      n->szer = s;
     34.      n->wyso = w;
     35.      n->next = next;
     36.  }
     37.  
     38.  void drukuj_liste(const Wezel* n) {
     39.      for ( ; n; n = n->next )
     40.          cout << n->szer << " " << n->wyso << "; ";
     41.      cout << endl;
     42.  }
     43.  
     44.  void drukuj_liste_odwrotnie(const Wezel* n) {
     45.      if (n == nullptr) return;  // pusta lista
     46.      if (n->next != nullptr)            ➍
     47.          drukuj_liste_odwrotnie(n->next);
     48.      cout << n->szer << " " << n->wyso << "; ";
     49.  }

W linii ➊ tworzymy obiekt A typu Wezel i od razu inicjujemy jego trzy składowe; taka składnia inicjowania dozwolona jest jak wiemy dla C-struktur, choć nie dla bardziej skomplikowanych struktur dopuszczanych przez C++. W linii następnej definiujemy dwa obiekty struktury —  B i  D — oraz wskaźnik do obiektów tej struktury head. W linii ➋ alokujemy na stercie jeszcze jeden obiekt; adres zwrócony przez new przypisujemy do pC. Następnie wypełniamy utworzone obiekty danymi za pomocą funkcji wstaw_dane. Pobiera ona adres obiektu do wypełnienia, dwie liczby typu double jako dane oraz adres innego obiektu, który ma być wartością składowej next i wskazywać na obiekt następny na liście. Zauważmy, że aby pobrać adres, stosujemy operator wyłuskania adresu ' &' dla A, B i  D, ale nie dla obiektu wskazywanego przez pC: pC jest zmienną wskaźnikową i już zawiera właśnie adres obiektu; sam obiekt wskazywany jest na stercie i w ogóle nie ma nazwy. Widzimy, że B zawiera adres A jako następującego po nim; dla obiektu wskazywanego przez pC następnym jest B, a dla D następnym jest *pC, czyli obiekt wskazywany przez pC. Sytuacja ta przedstawiona jest na rysunku:

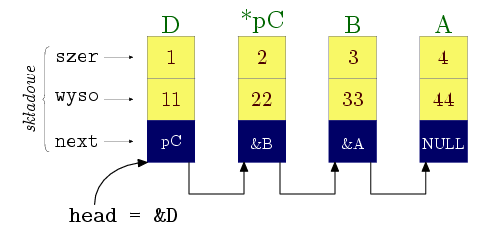
W linii ➌ zapamiętujemy w zmiennej head adres głowy listy. Zauważmy, że aby operować na liście, wystarczy nam ten adres: mając dostęp do pierwszego elementu, możemy w jego składowej next znaleźć adres następnego itd.

Jako przykład w programie zdefiniowane są dwie funkcje: drukuj_liste i  drukuj_liste_odwrotnie. Obie pobierają wyłącznie adres głowy listy. Pierwsza z nich przebiega po liście w pętli for drukując wartości danych; za każdym obrotem pętli wartość wskaźnika do obiektu z listy n zamieniana jest na ' n->next', aż wartością n stanie się nullptr, co nastąpi po dotarciu do elementu A.

Ciekawsza jest druga funkcja, drukuj_liste_odwrotnie. Jej zadaniem jest wydrukować informacje o elementach listy w odwrotnej kolejności: od ogona do głowy. Nie da się tego zrobić tak jak w poprzednim przypadku, bo nie możemy przechodzić listy do tyłu: elementy „nie znają” swych poprzedników. Rozwiązaniem jest rekurencja: z funkcji main wywołujemy drukuj_liste_odwrotnie dla głowy, czyli obiektu D. Funkcja jednak nie wypisuje informacji od razu, bo w linii ➍ następuje wywołanie dla następnika, a następnie dla jego następnika itd.; w końcu dla A (ogon listy) warunek z linii ➍ jest nieprawdziwy, zatem funkcja wypisuje informację i wraca do wywołania dla B, wypisuje informacje o  B i wraca do wywołania dla *pC itd. Widzimy, że wędrówkę do tyłu zapewnia nam zwijanie stosu podczas powrotów z wywołań funkcji:

    1 11; 2 22; 3 33; 4 44;
    4 44; 3 33; 2 22; 1 11;

Obiekt typu C-struktury może pełnić rolę zarówno argumentu funkcji, jak i wartości zwracanej przez funkcję. Trzeba jednak pamiętać, że przesyłanie obiektów do i z funkcji może być bardzo nieefektywne, jeśli obiekty są duże. W takich przypadkach należy raczej przesyłać wskaźniki (lub referencje) i starać się nie przenosić i nie kopiować samych obiektów. To samo dotyczy oparacji na tablicach obiektów: często lepiej jest operować raczej na tablicach wskaźników do obiektów.

Na przykład w poniższym programie obiekty struktury Krol zajmują co najmniej 44 bajty (40 na imie i 4 na ur), a wskaźniki do nich tylko 4 (lub 8):

      1.  #include <iostream>
      2.  #include <iomanip>   /* setw */
      3.  using namespace std;
      4.  
      5.  struct Krol{
      6.      int   ur;
      7.      char  imie[40];
      8.  };
      9.  
     10.  void insertionSort(Krol*[],int);
     11.  
     12.  int main() {
     13.      Krol zygmunt   = {1467,               "Zygmunt Stary"},
     14.           michal    = {1640, "Michal Korybut Wisniowiecki"},
     15.           wladyslaw = {1351,          "Wladyslaw Jagiello"},
     16.           anna      = {1523,            "Anna Jagiellonka"},
     17.           jan       = {1459,                "Jan Olbracht"};
     18.  
     19.      Krol* krolowie[] = { &zygmunt, &michal, &wladyslaw, ➊
     20.                           &anna,    &jan};
     21.  
     22.      const int ile = sizeof(krolowie)/sizeof(Krol*);
     23.  
     24.      cout << "sizeof(Krol ) = " << sizeof(Krol ) << endl;
     25.      cout << "sizeof(Krol*) = " << sizeof(Krol*) << endl
     26.                                                  << endl;
     27.      insertionSort(krolowie, ile);
     28.  
     29.      for ( int i =0; i < ile; i++ )                      ➋
     30.          cout << setw(28) << krolowie[i]->imie
     31.               << setw(5)  << krolowie[i]->ur << endl;
     32.  }
     33.  
     34.  void insertionSort(Krol* a[], int wymiar) {
     35.      if ( wymiar <= 1 ) return;
     36.  
     37.      for ( int i = 1 ; i < wymiar ; ++i ) {
     38.          int j = i;
     39.          Krol* v = a[i];
     40.          while ( j >= 1 && v->ur < a[j-1]->ur ) {        ➌
     41.              a[j] = a[j-1];                              ➍
     42.              j--;
     43.          }
     44.          a[j] = v;
     45.      }
     46.  }

Zatem, jeśli chcemy posortować królów według dat ich urodzenia, lepiej posortować tablicę wskaźników do obiektów ich reprezentujących, niż same te obiekty. Sortowanie bowiem łączy się z kopiowaniem i przenoszeniem elementów; lepiej jest więc kopiować wskaźniki niż czterdziestocztero-bajtowe obiekty. W linii ➊ budujemy zatem tablicę wskaźników i przesyłamy ją do funkcji sortującej. W funkcji sortującej, w linii ➌, widzimy, że kryterium sortowania jest wartość składowej ur obiektu wskazywanego przez wskaźnik będący elementem tablicy. Natomiast przestawiamy i kopiujemy tylko wskaźniki (jak w linii ➍), a nie wskazywane przez nie obiekty. Mimo to cel został osiągnięty: możemy wypisać imiona królów posortowane według roku urodzenia (➋):

    sizeof(Krol ) = 44
    sizeof(Krol*) = 8

              Wladyslaw Jagiello 1351
                    Jan Olbracht 1459
                   Zygmunt Stary 1467
                Anna Jagiellonka 1523
     Michal Korybut Wisniowiecki 1640

Można, a czasem trzeba, zadeklarować strukturę (unię, klasę) bez jej definiowania. Nie jest wtedy znany rozmiar obiektów tej struktury, więc jest to typ niekompletny. Taka deklaracja nazywa się zapowiadającą. Dzięki niej możemy korzystać z nazwy tego typu wszędzie tam, gdzie nie jest wymagany rozmiar obiektu, a więc np. do definiowania wskaźników do obiektów tego typu. Oczywiście, tylko definiowania, ale nie np. inicjowania, bo żeby taki wskaźnik zainicjować, musiałby istnieć obiekt, a ten możemy utworzyć dopiero po pełnym zdefiniowaniu struktury, kiedy będzie znany rozmiar jej obiektów.

Sytuacja, kiedy taka deklaracja zapowiadająca jest konieczna zachodzi, gdy jedna struktura zawiera, jako pola, wskaźniki do drugiej struktury, a ta druga – wskaźniki do tej pierwszej. Tak więc fragment

      1.      struct AA {
      2.          BB *b; // NIE
      3.          // ...
      4.      };
      5.  
      6.      struct BB {
      7.          AA *a;
      8.          // ...
      9.      }

       struct Nazwa;

      1.      struct BB;
      2.  
      3.      struct AA {
      4.          BB *b;
      5.          // ...
      6.      };
      7.  
      8.      struct BB {
      9.          AA *a;
     10.          // ...
     11.      }

Jako przykład rozpatrzmy program:

      1.  #include <iostream>
      2.  #include <cstring>   // strcpy
      3.  using namespace std;
      4.  
      5.  struct Husband;
      6.  struct Wife;
      7.  
      8.  void prinfo(const Husband*);
      9.  void prinfo(const Wife*);
     10.  
     11.  struct Wife {
     12.      Husband *hus;
     13.      char name[20];
     14.  } honoratka = { 0, "Honoratka" } ;
     15.  
     16.  struct Husband {
     17.      Wife *wif;
     18.      char name[20];
     19.  } antoni  = { 0 } ;
     20.  
     21.  int main() {
     22.      strcpy(antoni.name, "Antoni");           ➊
     23.  
     24.      antoni.wif    = &honoratka;
     25.      honoratka.hus = &antoni;
     26.  
     27.      Husband zenobiusz  = { 0, "Zenobiusz" };
     28.      Wife    celestynka = { 0, "Celestynka"};
     29.  
     30.      prinfo(&antoni);
     31.      prinfo(&honoratka);
     32.      prinfo(&zenobiusz);
     33.      prinfo(&celestynka);
     34.  }
     35.  
     36.  void prinfo(const Husband *h) {
     37.      cout << "Mezczyzna: " << h->name;
     38.      if ( h->wif )
     39.          cout << "; zona "
     40.               << h->wif->name << "\n";        ➋
     41.      else
     42.          cout << "; (kawaler)\n";
     43.  }
     44.  
     45.  void prinfo(const Wife *w) {
     46.      cout << "Kobieta:   " << w->name;
     47.      if ( w->hus )
     48.          cout << "; maz "
     49.               << (*((*w).hus)).name << "\n";  ➌
     50.      else
     51.          cout << "; (panna)\n";
     52.  }

Na początku deklarujemy dwie struktury: Husband i  Wife. Dzięki temu możemy zadeklarować funkcje prinfo których typem parametru są wskaźniki do obiektów Husband i  Wife (nie możemy na razie zdefiniować tych funkcji, bo w jej treści używać będziemy nazw pól tych struktur, a te nie są na razie znane). Zauważmy, że deklarujemy dwie funkcje o tej samej nazwie. Różnią się one jednak wystarczająco typem parametru, więc takie przeciążenie jest legalne.

Dalej definiujemy struktury Husband i  Wife, przy czym mamy tu właśnie do czynienia z przypadkiem, gdy jedna struktura zawiera, jako pole, wskaźnik do drugiej struktury, a ta druga – wskaźnik do tej pierwszej. Zatem deklaracja zapowiadająca była tu niezbędna. Zauważmy też, że nawet po tej deklaracji niemożliwe byłoby, aby struktura Wife zawierała jako pole obiekt (a nie wskaźnik) typu Husband, a struktura Husband obiekt typu Wife. Oznaczałoby to bowiem, że obiekt typu Wife zawierałby obiekt typu Husband, który z kolei zawierałby obiekt typu Wife, który z kolei ...i tak ad infinitum. Funkcja strcpy z linii ➊ służy do kopiowania C-napisów i poznamy ją dokładniej w rozdziale o napisach . Dalszy ciąg programu jest już zrozumiały; jego rezultat:

    Mezczyzna: Antoni; zona Honoratka
    Kobieta:   Honoratka; maz Antoni
    Mezczyzna: Zenobiusz; (kawaler)
    Kobieta:   Celestynka; (panna)

       h->wif->name

       (*((*w).hus)).name

---

Wstecz: 13. C-struktury i unie W górę: 13. C-struktury i unie Dalej: 13.2 Unie