


Next: The Skyrme HFB method
Up: The HFB method
Previous: The HFB method
In terms of the density matrix  and pairing tensor
and pairing tensor  ,
defined as
,
defined as
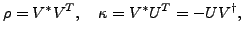 |
(7) |
the HFB energy is expressed as an energy functional:
where
The variation of the HFB energy (8) with respect to  and
and  yields the HFB equations:
yields the HFB equations:
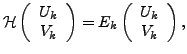 |
(11) |
where
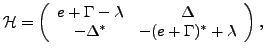 |
(12) |
 and
and  are the
are the  th columns of matrices
th columns of matrices  and
and  ,
respectively, and
,
respectively, and  is a positive quasiparticle energy eigenvalue.
Since the HFB state
is a positive quasiparticle energy eigenvalue.
Since the HFB state
 violates the particle-number symmetry,
the Fermi energy
violates the particle-number symmetry,
the Fermi energy  is introduced to fix the average particle number.
is introduced to fix the average particle number.



Next: The Skyrme HFB method
Up: The HFB method
Previous: The HFB method
Jacek Dobaczewski
2006-10-13
![]() and pairing tensor
and pairing tensor ![]() ,
defined as
,
defined as