The HFB method

The many-body Hamiltonian of a system of fermions is usually expressed in terms of a set of annihilation and creation operators $(c,c^{\dagger })$:

$$H = \sum_{nn'}e_{nn'}~c_{n}^{\dagger }c_{n'}$$

$$+ \tfrac{1}{4}\sum_{nn'mm'}V_{nn'mm'}~c_{n}^{\dagger }c_{n'}^{\dagger }c_{m'}c_{m},$$ (1)

where

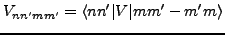$$V_{nn'mm'}=\langle nn'\vert V\vert mm'-m'm\rangle$$ (2)

are the anti-symmetrized two-body interaction matrix-elements.

In the HFB method, the ground-state wave function is the quasiparticle vacuum $\vert\Phi \rangle ,$ defined as $\alpha _{k}\vert\Phi \rangle =0$, where the quasiparticle operators $(\alpha ,\alpha^{\dagger })$ are connected to the original particle operators via the Bogoliubov transformation

$$\quad \quad \alpha_{k} = \sum_{n}\left( U_{nk}^{\ast }c_{n}+V_{nk}^{\ast }c_{n}^{\dagger }\right) ,$$ (3)

$$\quad \quad \alpha_{k}^{\dagger } = \sum_{n}\left( V_{nk}c_{n}+U_{nk}c_{n}^{\dagger }\right),$$ (4)

where the matrices $U$ and $V$ satisfy the unitarity and completeness relations:

$$U^{\dagger }U+V^{\dagger }V=I, UU^{\dagger }+V^{\ast }V^{T}=I,$$ (5)

$$U^{T}V+V^{T}U=0, UV^{\dagger }+V^{\ast }U^{T}=0.$$ (6)