| = | 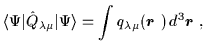 |
(82) | |
| = |  |
(83) |
The electric and magnetic moments are defined as
Similarly, the mean value of the k-component of total angular momentum
(in units of ![]() )
reads
)
reads
We may now combine symmetry properties of densities ![]() ,
,
![]() ,
and
,
and
![]() ,
Table 3, with those of multipole
operators, Table 5, to obtain symmetry conditions obeyed by
the electric and magnetic moments, and by the average angular
momenta, for given conserved symmetries of the D
,
Table 3, with those of multipole
operators, Table 5, to obtain symmetry conditions obeyed by
the electric and magnetic moments, and by the average angular
momenta, for given conserved symmetries of the D
![]() or D
or D
![]() groups. In doing
so, we have to remember that since the electric multipole operators
are time-even, the corresponding electric moments depend only on the
time-even component of the density matrix, as given in
Eq. (84). This is so irrespective of whether the
time reversal is, or is not a conserved symmetry, or whether the
system contains even or odd number of fermions. Therefore, the
time reversal does not impose any condition on the electric multipole
moments. On the other hand, with the time-reversal symmetry
conserved, which may occur only for even systems, all magnetic
moments and average angular momenta must vanish, because they depend
only on the time-odd component of the density matrix, Eqs. (85)
and (86).
groups. In doing
so, we have to remember that since the electric multipole operators
are time-even, the corresponding electric moments depend only on the
time-even component of the density matrix, as given in
Eq. (84). This is so irrespective of whether the
time reversal is, or is not a conserved symmetry, or whether the
system contains even or odd number of fermions. Therefore, the
time reversal does not impose any condition on the electric multipole
moments. On the other hand, with the time-reversal symmetry
conserved, which may occur only for even systems, all magnetic
moments and average angular momenta must vanish, because they depend
only on the time-odd component of the density matrix, Eqs. (85)
and (86).
| k |
|
|
|
| ||||||||||||||||||
| x |
| = |
|
|
| = |
|
|
| = |
|
| = |
|
||||||||
| x |
| = |
|
|
| = |
|
|
| = | - |
|
| = |
|
|||||||
| y |
| = |
|
|
| = |
|
|
| = |
|
|
| = |
|
|
||||||
| y |
| = |
|
|
| = |
|
|
| = |
|
|
| = |
|
|
||||||
| z |
| = |
|
|
| = |
|
|
| = |
|
|
| = |
|
|
||||||
| z |
| = |
|
|
| = |
|
|
| = |
|
|
| = |
|
|
||||||
| x |
| = |
|
|
| = |
|
|
| = |
|
|
| = |
|
|
||||||
| x |
| = |
|
|
| = |
|
|
| = |
|
|
| = |
|
|
||||||
| y |
| = |
|
|
| = |
|
|
| = |
|
| = |
|
||||||||
| y |
| = |
|
|
| = |
|
|
| = | - |
|
| = |
|
|||||||
| z |
| = |
|
|
| = |
|
|
| = |
|
|
| = |
|
|
||||||
| z |
| = |
|
|
| = |
|
|
| = |
|
|
| = |
|
|
||||||
For the conserved parity, one obtains the standard conditions:
Within the standard phase convention of Eq. (80),
only a conservation of the y-T-simplex symmetry,
![]() ,
enforces
the reality of all multipole electric and magnetic moments.
In such a case, the lower part of Table 6 gives at a glance
all the multipole moments which must vanish whenever any other
symmetry is additionally conserved; these are those
for which the phase factors are negative.
On the other hand,
a conservation of the x-T-simplex symmetry,
,
enforces
the reality of all multipole electric and magnetic moments.
In such a case, the lower part of Table 6 gives at a glance
all the multipole moments which must vanish whenever any other
symmetry is additionally conserved; these are those
for which the phase factors are negative.
On the other hand,
a conservation of the x-T-simplex symmetry,
![]() ,
enforces the equality of
negative and positive magnetic components.
In this case, a conservation of any additional symmetry
puts to zero the multipole moments with
negative phase factors appearing in the upper part of the Table.
Of course, numerous other combinations of conserved symmetries
can be considered,
for example, a conservation of the y-simplex symmetry,
,
enforces the equality of
negative and positive magnetic components.
In this case, a conservation of any additional symmetry
puts to zero the multipole moments with
negative phase factors appearing in the upper part of the Table.
Of course, numerous other combinations of conserved symmetries
can be considered,
for example, a conservation of the y-simplex symmetry,
![]() ,
gives real electric moments and imaginary magnetic
moments.
,
gives real electric moments and imaginary magnetic
moments.
Since conditions listed in Table 6 depend only on the
parity of ![]() and on the parity of
and on the parity of ![]() ,
and since
condition (80) allows us to consider only non-negative
values of
,
and since
condition (80) allows us to consider only non-negative
values of ![]() ,
one has only six types of the symmetry properties of
multipole moments with respect to the D
,
one has only six types of the symmetry properties of
multipole moments with respect to the D
![]() or D
or D
![]() operators. These six
types are listed in Table 7 for electric and magnetic
moments. Column denoted by the identity operator
operators. These six
types are listed in Table 7 for electric and magnetic
moments. Column denoted by the identity operator ![]() gives
the properties resulting solely from condition (80),
while the remaining columns give properties of moments when one
of the non-identity D
gives
the properties resulting solely from condition (80),
while the remaining columns give properties of moments when one
of the non-identity D
![]() or D
or D
![]() operators is conserved.
operators is conserved.
In the same Table we also give symmetry properties of the
Cartesian components of the average angular momenta
Ik (86). Although the symmetry properties of
the angular momentum are identical to those of the dipole
magnetic moment, explicit values shown for its Cartesian
components allow for a simple visualization of a direction taken
by the angular-momentum vector when various D
![]() or D
or D
![]() operators are
conserved. In particular, one can see that a conservation of
any of the signature or simplex operators for a given axis enforces the
angular-momentum direction along that axis, while a
conservation of any T-signature or T-simplex operators
allows for a tilted angular momentum in the plane perpendicular
to the given axis, cf. Ref.[23].
On the other hand, none of these operators
may be conserved if the angular momentum is to be tilted beyond
any of the x-y, y-z, and z-x planes. Note, however,
that the above tilting conditions pertain to the reference frame,
and not to the principal axes of the mass distribution. An
appropriate choice of the reference frame, as discussed below,
has to be performed in
order to relate the conserved D
operators are
conserved. In particular, one can see that a conservation of
any of the signature or simplex operators for a given axis enforces the
angular-momentum direction along that axis, while a
conservation of any T-signature or T-simplex operators
allows for a tilted angular momentum in the plane perpendicular
to the given axis, cf. Ref.[23].
On the other hand, none of these operators
may be conserved if the angular momentum is to be tilted beyond
any of the x-y, y-z, and z-x planes. Note, however,
that the above tilting conditions pertain to the reference frame,
and not to the principal axes of the mass distribution. An
appropriate choice of the reference frame, as discussed below,
has to be performed in
order to relate the conserved D
![]() or D
or D
![]() operators to the direction
of Ik with respect to the mass principal
axes.
operators to the direction
of Ik with respect to the mass principal
axes.
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
| Q10,Q30,Q50 |
R | R | 0 | 0 | 0 | 0 | R | R | 0 | 0 | R | R | R | R | 0 | 0 |
| Q11,Q31,Q33 |
C | C | 0 | 0 | R | R | I | I | I | I | R | R | 0 | 0 | C | C |
| Q20,Q40,Q60 |
R | R | R | R | R | R | R | R | R | R | R | R | R | R | R | R |
| Q21,Q41,Q43 |
C | C | C | C | I | I | I | I | R | R | R | R | 0 | 0 | 0 | 0 |
| Q22,Q42,Q44 |
C | C | C | C | R | R | R | R | R | R | R | R | C | C | C | C |
| Q32,Q52,Q54 |
C | C | 0 | 0 | I | I | R | R | I | I | R | R | C | C | 0 | 0 |
| M10,M30,M50 |
R | 0 | R | 0 | 0 | R | 0 | R | 0 | R | 0 | R | R | 0 | R | 0 |
| M11,M31,M33 |
C | 0 | C | 0 | R | I | R | I | I | R | I | R | 0 | C | 0 | C |
| M20,M40,M60 |
R | 0 | 0 | R | R | 0 | 0 | R | R | 0 | 0 | R | R | 0 | 0 | R |
| M21,M41,M43 |
C | 0 | 0 | C | I | R | R | I | R | I | I | R | 0 | C | C | 0 |
| M22,M42,M44 |
C | 0 | 0 | C | R | I | I | R | R | I | I | R | C | 0 | 0 | C |
| M32,M52,M54 |
C | 0 | C | 0 | I | R | R | R | I | R | I | R | C | 0 | C | 0 |
| Ix | R | 0 | R | 0 | R | 0 | R | 0 | 0 | R | 0 | R | 0 | R | 0 | R |
| Iy | R | 0 | R | 0 | 0 | R | 0 | R | R | 0 | R | 0 | 0 | R | 0 | R |
| Iz | R | 0 | R | 0 | 0 | R | 0 | R | 0 | R | 0 | R | R | 0 | R | 0 |
Independently of any D
![]() or D
or D
![]() symmetry breaking, the reference frame in
the space coordinates can be chosen in such way that some of the moments
have simple forms. For example, a shift of the reference frame can
bring all electric dipole moments to zero (this corresponds to using
the center-of-mass system of reference), i.e.,
symmetry breaking, the reference frame in
the space coordinates can be chosen in such way that some of the moments
have simple forms. For example, a shift of the reference frame can
bring all electric dipole moments to zero (this corresponds to using
the center-of-mass system of reference), i.e.,
On the other hand, for some conserved symmetries, these
conditions can be automatically satisfied. For example,
conservation of the D
![]() group (i.e., simultaneous invariance
with respect to operators
group (i.e., simultaneous invariance
with respect to operators ![]() ,
,
![]() ,
and
,
and
![]() )
ensures that the center-of-mass (89) and
principal-axes (90) conditions are automatically
satisfied, see Table 7. Therefore, the breaking of the
D
)
ensures that the center-of-mass (89) and
principal-axes (90) conditions are automatically
satisfied, see Table 7. Therefore, the breaking of the
D
![]() or D
or D
![]() symmetries may have non-trivial physical consequences
only for higher electric moments; starting from Q30, if
the parity is broken, or starting from Q41, for example,
if the parity is conserved. In other words, the D
symmetries may have non-trivial physical consequences
only for higher electric moments; starting from Q30, if
the parity is broken, or starting from Q41, for example,
if the parity is conserved. In other words, the D
![]() or D
or D
![]() symmetry breaking will not lead to new classes of
low-multipolarity shapes. Nevertheless, such symmetry
breaking will immediately be reflected in values of magnetic
moments, whenever the time reversal is broken too.
symmetry breaking will not lead to new classes of
low-multipolarity shapes. Nevertheless, such symmetry
breaking will immediately be reflected in values of magnetic
moments, whenever the time reversal is broken too.