


Next: Comparison with data
Up: Probing the densities of
Previous: Models of structure of
Scattering from Hydrogen - gedanken results
We have used the canonical single-particle
wave functions for all of the Sn isotopes to fold an
effective NN interaction and thus generate optical potentials for
use in modified versions of the scattering program
DWBA98 [18]. Those optical potentials are complex and non-local
since they can be written in coordinate space with
 ,
as
,
as
 |
(1) |
where the direct UD and non-local exchange UE terms are
| UD |
= |
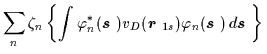 |
|
| UE |
= |
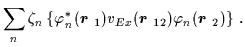 |
(2) |
Here vD and vEx are combinations of the components of the
effective NN interactions,  are ground state one body
density matrices (effectively bound state shell occupancies), and
are ground state one body
density matrices (effectively bound state shell occupancies), and
 are single nucleon bound states. All details and
the prescription of solution of the associated nonlocal Schrödinger
equations are given in the recent review [16]. The results to
be discussed herein have been obtained by solving the actual nonlocal
Schrödinger equations defined with potentials as given by
Eq. (1). For the present calculations, the effective NNinteractions have been defined by their mapping to the BBG gmatrices of the BonnB NN interaction [25].
We consider the elastic scattering of 200 MeV protons from each of the
even mass Sn isotopes (A = 100 to 176). By inverse kinematics the
cross sections we determine are also those for the scattering of
200A MeV Sn ions from hydrogen; some of which can be, or may soon
be, obtained in sufficient numbers to form a radioactive ion beam for
experiment. The choice of 200 MeV was made, not only because the
effective force at this energy has been used in many successful
predictions of actual scattering data from stable nuclei [16]
but also since that energy provided data from 208Pb in which a
clear signature of the neutron density profile has been
found [15].
are single nucleon bound states. All details and
the prescription of solution of the associated nonlocal Schrödinger
equations are given in the recent review [16]. The results to
be discussed herein have been obtained by solving the actual nonlocal
Schrödinger equations defined with potentials as given by
Eq. (1). For the present calculations, the effective NNinteractions have been defined by their mapping to the BBG gmatrices of the BonnB NN interaction [25].
We consider the elastic scattering of 200 MeV protons from each of the
even mass Sn isotopes (A = 100 to 176). By inverse kinematics the
cross sections we determine are also those for the scattering of
200A MeV Sn ions from hydrogen; some of which can be, or may soon
be, obtained in sufficient numbers to form a radioactive ion beam for
experiment. The choice of 200 MeV was made, not only because the
effective force at this energy has been used in many successful
predictions of actual scattering data from stable nuclei [16]
but also since that energy provided data from 208Pb in which a
clear signature of the neutron density profile has been
found [15].
In Fig. 10, the differential cross sections for the
scattering from all of the even mass Sn isotopes are plotted to
 in the center of mass by which angle the cross section
magnitude is O(0.1) mb/sr. The SLy4 model calculations were used to
specify the OBDME and single particle wave functions by which the
optical potentials were generated. Several trends are noticed in the
differential cross section as the mass is increased. The first three
minima tend to forward angles and the intervening (first) maximum
becomes more pronounced as the neutron number increases. There are
model signatures in these results for scattering angles
in the center of mass by which angle the cross section
magnitude is O(0.1) mb/sr. The SLy4 model calculations were used to
specify the OBDME and single particle wave functions by which the
optical potentials were generated. Several trends are noticed in the
differential cross section as the mass is increased. The first three
minima tend to forward angles and the intervening (first) maximum
becomes more pronounced as the neutron number increases. There are
model signatures in these results for scattering angles  (and higher) that have magnitudes still possible to be detected in
experiment. Since the p-n force (isoscalar 3S1 channel) is the
strongest, such effects primarily reflect attributes of the neutron
density variation in the surface region of the nuclei. They are
revealed also by considering the ratio to Rutherford values which are
shown in Fig. 11.
(and higher) that have magnitudes still possible to be detected in
experiment. Since the p-n force (isoscalar 3S1 channel) is the
strongest, such effects primarily reflect attributes of the neutron
density variation in the surface region of the nuclei. They are
revealed also by considering the ratio to Rutherford values which are
shown in Fig. 11.
Figure 10:
The differential cross section for the
elastic scattering of 200 MeV protons from the Sn isotopes. The SLy4
model was used in forming the optical potentials.
 |
Figure 11:
The results of Fig.10 shown as
ratios to Rutherford scattering.
 |
Therein the marked change in the magnitudes of results for the isotope
in the mass range 110 to 120 as is the trend of peak and valley
magnitudes to smaller momentum transfer as mass increases.
If ever exotic Sn nuclei can be formed as a radioactive beam for
scattering from polarized hydrogen targets, spin measurables such as
the spin rotation, Q, could be found. That quantity from the SLy4
model calculations is shown in Fig. 12.
Figure 12:
The spin observable Q from 200 MeV proton
scattering with the Sn isotopes.
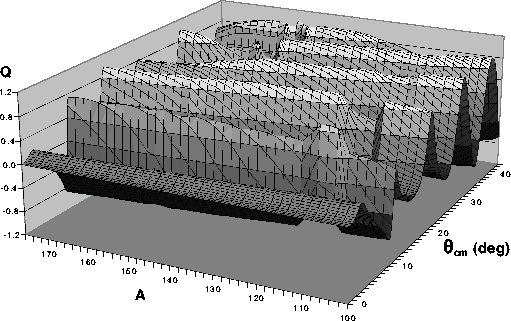 |
The graphical view has been rotated from the aspect given with the
cross section results to show more readily the model dependencies in
our calculated results. For clarity, the mass variation now is shown
across the page while the scattering angle variation occurs into the
page. Again the prime feature of these results is the trend with mass
for the peaks and valleys to smaller momentum transfer values, but
there is also a strong model dependence of magnitudes, notably in the
mass range 110 to 120.



Next: Comparison with data
Up: Probing the densities of
Previous: Models of structure of
Jacek Dobaczewski
2002-05-06
![]() ,
as
,
as
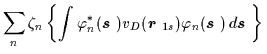
![]() in the center of mass by which angle the cross section
magnitude is O(0.1) mb/sr. The SLy4 model calculations were used to
specify the OBDME and single particle wave functions by which the
optical potentials were generated. Several trends are noticed in the
differential cross section as the mass is increased. The first three
minima tend to forward angles and the intervening (first) maximum
becomes more pronounced as the neutron number increases. There are
model signatures in these results for scattering angles
in the center of mass by which angle the cross section
magnitude is O(0.1) mb/sr. The SLy4 model calculations were used to
specify the OBDME and single particle wave functions by which the
optical potentials were generated. Several trends are noticed in the
differential cross section as the mass is increased. The first three
minima tend to forward angles and the intervening (first) maximum
becomes more pronounced as the neutron number increases. There are
model signatures in these results for scattering angles ![]() (and higher) that have magnitudes still possible to be detected in
experiment. Since the p-n force (isoscalar 3S1 channel) is the
strongest, such effects primarily reflect attributes of the neutron
density variation in the surface region of the nuclei. They are
revealed also by considering the ratio to Rutherford values which are
shown in Fig. 11.
(and higher) that have magnitudes still possible to be detected in
experiment. Since the p-n force (isoscalar 3S1 channel) is the
strongest, such effects primarily reflect attributes of the neutron
density variation in the surface region of the nuclei. They are
revealed also by considering the ratio to Rutherford values which are
shown in Fig. 11.
