Minute No. 4, the Quantum Field Theory

Quantum field theory Wei99 performs quantization of classical fields in a very much the same way as the quantum mechanics performs quantization of classical coordinates. The field wave function now becomes a functional $\Psi[\psi({x})]$ of the field $\psi({x})$, and the quantum fields and the quantum conjugate momenta are

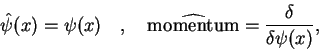$$\hat{\psi}(x) = \psi(x)\quad,\quad \widehat{\mbox{momentum}} = \frac{\delta}{\delta \psi(x)} ,$$ (13)

where $\delta$ denotes the functional derivative. The Schrödinger equation (9) now becomes the set of infinite number of differential equations - a pretty complicated thing. I somehow hesitate to write that the rest is just a technicality of how to solve it. In principle, nothing special has happened. The same rules have been applied and an analogous, albeit much more complicated, set of equations emerged. However, we are very, very far from even approaching a possibility of exact solutions of this set. We are not at all going to embark on discussing these questions here. Basic physical picture of the quantum field theory can be very well discussed in terms of its classical counterpart, and in terms of classical-field Lagrangian densities discussed during the third minute above. It as amazing how much can be said about properties of the micro-world by just specifying what are the symmetries and the basic couplings between the classical fields. Below we follow this way of presenting properties of strongly interacting systems.

The new, qualitatively different, element introduced by the quantum field theory is that particles now disappeared from our description of the physical world - there are only fields. One does not distinguish which is the object that ``exists'' and which is the object that ``transmits forces''. All fields have both these characteristics simultaneously; which field interacts with which, and in which way, is fully specified by the Lagrangian density.