Minute No. 2, the Quantum Mechanics

Quantum systems Mes71 are described by the wave function $\Psi(q_i,t)$ (complex function of coordinates $q_i$ and time $t$), and by the Hamilton operator $\hat{H}$ that can be obtained from the classical Hamiltonian by a procedure called quantization. We define operators that correspond to each classical object, e.g., the classical coordinates and momenta are quantized as,

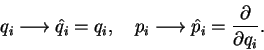$$q_i \longrightarrow \hat{q}_i = q_i,\quad p_i \longrightarrow \hat{p}_i = \frac{\partial}{\partial q_i} .$$ (7)

Then, the Hamilton operator is, more or less, obtained by inserting these operators into the classical Hamiltonian, i.e.,

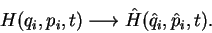$${H}({q}_i,{p}_i,t) \longrightarrow \hat{H}(\hat{q}_i,\hat{p}_i,t) .$$ (8)

This is not an exact science, because the function of operators cannot be uniquely defined for a given function of variables; one has to also define the order in which the operators act. Well, in fact the quantization provides us only with general rules on how to start the quantum mechanics based on our knowledge of the classical mechanics. One can also subscribe to the point of view that we must axiomatically define the quantum system by specifying its Hamilton operator. Once this is done, the time evolution of the system (of its wave function) is given by the Schrödinger equation,

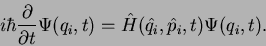$$i\hbar\frac{\partial}{\partial t}\Psi(q_i,t) = \hat{H}(\hat{q}_i,\hat{p}_i,t) \Psi(q_i,t) .$$ (9)

This leads to a set coupled differential equations that can be, in principle, solved once the initial conditions $\Psi(q_i,t$=0) are known. One thus obtains the complete past and future history of the system $\Psi(q_i,t)$. The rest is just a technicality ;) of how to solve differential equations.

Quantum mechanics also adds a pivotal element to our understanding of how our world works, namely, the probabilistic interpretation. In classical mechanics, once our Euler-Lagrange equations give us the set of coordinates $q_i$ at time $t$, the experiment performed at time $t$ to find the system at point $q_i$ yields one possible answer: the system is there. In quantum mechanics, the same experiment yields the answer that the system is within volume ${\rm d}{V}$ around $q_i$ with probability $\vert\Psi(q_i,t)\vert^2{\rm d}{V}$ and the answer that it is not there, with probability $1-\vert\Psi(q_i,t)\vert^2{\rm d}{V}$. Hélas, it seems that the world is just like that, nothing is certain any more. However, at least the probabilities of obtaining given experimental answers can be rigorously calculated.