Basics of energy density theory

Many calculations performed with the Skyrme interaction can be viewed as energy-density theory in the spirit of the Hohenberg-Kohn-Sham approach [15], originally introduced for many-electron systems. Nowadays, energy density theory is a standard tool in atomic, molecular, cluster, and solid-state physics [16], as well as in nuclear physics [17]. The starting point is an energy functional ${\cal E}$ of all local densities and currents $\rho$, $\tau$, $\stackrel{\leftrightarrow}{J}$, $\vec{s}$, $\vec{T}$, and $\vec{j}$ that can be constructed from the most general single-particle density matrix

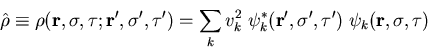$$\hat\rho \equiv \rho (\vec{r}, \sigma, \tau; \vec{r}', \sigm... ... (\vec{r}', \sigma', \tau') \; \psi_k (\vec{r}, \sigma, \tau)$$ (1)

(see Appendix 7 for more details), where $\vec{r}$, $\sigma$, and t are the spatial, spin, and isospin coordinates of the wave function. The Hohenberg-Kohn-Sham approach maps the nuclear many-body problem for the ``real'' highly correlated many-body wave function on a system of independent particles in so-called Kohn-Sham orbitals $\psi_k$. The equations of motion for $\psi_k$ are derived from the variational principle

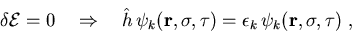$$\delta {\cal E} = 0 \quad \Rightarrow \quad \hat{h} \, \psi_... ...\sigma, \tau) = \epsilon_k \, \psi_k (\vec{r}, \sigma, \tau)~,$$ (2)

where the single-particle Hamiltonian $\hat{h}$ is the sum of the kinetic term $\hat{t}$ and the self-consistent potential $\Gamma$ that is calculated from the density matrix

$$\hat{h} = \frac{\delta {\cal E}}{\delta \hat\rho} = \hat{t} + \hat\Gamma [\hat\rho] \quad .$$ (3)

The existence theorem for the effective energy functional makes no statement about its structure. The theoretical challenge is to find an energy functional that incorporates all relevant physics with as few free parameters as possible. The density functional approach as used here is equivalent to the local density approximation to the nuclear G matrix [18].

The energy functional investigated here in detail describes the particle-hole channel of the effective interaction only. For the treatment of pairing correlations, the energy functional has to be complemented by an effective particle-particle interaction that is constructed in a similar way from the pairing density matrix; see [19] for details. We use here the simplest functional proportional to the square of the local pair density with the coupling constants given in [11].