Uncertain Extrapolations

Experimentation with radioactive nuclear beams is expected to expand the range of known nuclei. That is, by going to nuclei with extreme N/Z ratios, one can magnify the isospin-dependent terms of the effective interaction (which are small in ``normal" nuclei). The hope is that after probing these terms at the limits of extreme isospin, we can later go back to the valley of stability and improve the description of normal nuclei. In addition to nuclear structure interest, the understanding of effective interactions in the neutron-rich and proton-rich environment is important for astrophysics and cosmology.

  

Figure 2: Predicted two-neutron separation energies for the even-even Sn isotopes using several microscopic models based on effective density-dependent nucleon-nucleon interactions (from Refs. [6,7]).

Figure 2 illustrates difficulties with making theoretical extrapolations into neutron-rich territory. It shows the two-neutron separation energies for the even-even Sn isotopes calculated in several microscopic models based on different effective interactions. Clearly, the differences between forces are greater in the region of ``terra incognita" than in the region where masses are known (an effect half-jokingly called ``asymptotic freedom"). Therefore, the uncertainty due to the largely unknown isospin dependence of the effective force (in both particle-hole and particle-particle channels) gives an appreciable theoretical ``error bar" for the position of the drip line. Unfortunately, the results presented in Fig. 2 do not tell us much about which of the forces discussed should be preferred since one is dealing with dramatic extrapolations far beyond the region known experimentally. However, a detailed analysis of the force dependence of results may give us valuable information on the relative importance of various force parameters. Moreover, it is obvious that the experimental data on nuclei near stability do not sufficiently constrain results for exotic nuclei. Therefore, further measurements in neutron-rich systems are of vital importance for the development of theoretical descriptions. We note in passing that attempts to derive the effective interactions from first principles may lead to even larger uncertainties for exotic nuclei (see recent analysis in Ref.[8]).

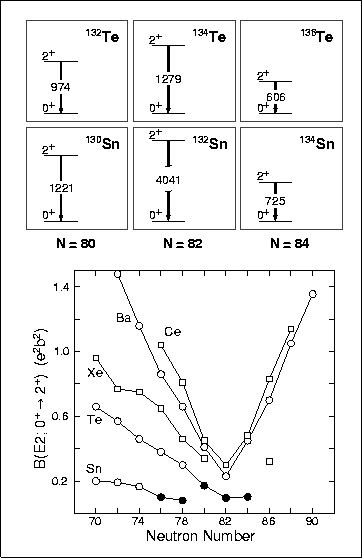
Figure 3 demonstrates that one does not need to go all the way to the neutron drip line to see deviations from well-established trends. Indeed, the differences between various models describing masses of Sn isotopes show up just above N=82. Interestingly, experimental data around ¹³²Sn exhibit an unusual pattern as one crosses N=82. Namely, there is a striking asymmetry in the position of 2⁺₁levels in N=80 and 82 isotopes of Sn and Te, and the $B(E2;0^+ \rightarrow 2^+_1)$rate in ¹³⁶Te stays unexpectedly low [9], defying common wisdom that the decrease in E_2⁺1 in open-shell nuclei must imply the increase in $B(E2;0^+ \rightarrow 2^+_1)$. So far, there is no satisfactory explanation for the pattern shown in Fig. 3. What is clear, however, is that one must be prepared for many surprises when entering the neutron-rich territory.

  

Figure 3: Top: 2⁺₁ levels in N=80,82,84 Sn and Te isotopes. Bottom: Values of $B(E2;0^+ \rightarrow 2^+_1)$ for even-even Sn, Te, Xe, Ba, and Ce isotopes around neutron number N=82. Filled symbols indicate the recent RNB measurements at the HRIBF facility at ORNL (from Ref. [9]).