


Next: Direct Coulomb energy in
Up: The NLO potentials, fields,
Previous: Matrix elements of the
The total potential energy in the spherical symmetry
The energy related to
one term in the energy density (38) reads
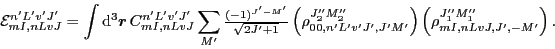 |
(110) |
We carry out the derivation for arbitrary values
of multipole components, that is for
 ,
while the standard HF total energy in spherical symmetry corresponds to the particular
case of
,
while the standard HF total energy in spherical symmetry corresponds to the particular
case of
 . In the general case,
the result corresponds to the energy matrix element between two multipole components,
and allows one to calculated the total energy for the density matrix being a linear
combination of multipole components, that is, for a deformed state.
. In the general case,
the result corresponds to the energy matrix element between two multipole components,
and allows one to calculated the total energy for the density matrix being a linear
combination of multipole components, that is, for a deformed state.
After using the definition of reduced density in Eq. (102),
the energy (116) becomes equal to:
By using the multiplication theorem for the spherical harmonics, one obtains the expression
which, for density-independent coupling constants, can be integrated over  and
and  .
After summing up the Clebsh-Gordan coefficients, one obtains:
.
After summing up the Clebsh-Gordan coefficients, one obtains:
One thus obtains the correct result that for density-independent
coupling constants, the potential energy is diagonal
in different multipoles.
When the coupling constants do depend on density, the angular integral cannot be performed,
and a similar derivation gives the general result:
For the spherical case, one has
 , which implies
, which implies  , and both
expressions (118) and (119) reduce to:
, and both
expressions (118) and (119) reduce to:
For density-dependent terms, such as those in Eqs. (62) and (63),
the total energy reads
where the density
 depends on the reduced density as:
depends on the reduced density as:
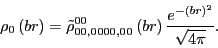 |
(116) |



Next: Direct Coulomb energy in
Up: The NLO potentials, fields,
Previous: Matrix elements of the
Jacek Dobaczewski
2010-01-30



![]() , which implies
, which implies ![]() , and both
expressions (118) and (119) reduce to:
, and both
expressions (118) and (119) reduce to:
