Potentials

The potential energy to be varied over the wave functions is given in Ref. [4] and reads

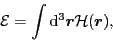$${\cal E} = \int {\rm d}^3\vec{r} {\cal H}(\vec{r}),$$ (36)

for

$${\cal H}(\vec{r}) = \sum_{{n'L'v'J'}\atop{mI,nLvJ}} C^{n'L'v'J'}_{mI,nLvJ}\, [\rho_{n'L'v'J'}(\vec{r})[D_{mI}\rho_{nLvJ}(\vec{r})]_{J'}]_0$$

$$= \sum_{{n'L'v'J'M'}\atop{mI,nLvJ}} \!\!\! C^{n'L'v'J'}_{mI,nLvJ} {... ...t{2J'+1}}}} \, \rho_{n'L'v'J'M'}(\vec{r})[D_{mI}\rho_{nLvJ}(\vec{r})]_{J',-M'},$$ (37)

where $C^{n'L'v'J'}_{mI,nLvJ}$ are the coupling constants and $\rho_{nLvJ}(\vec{r})$ are the primary densities:

$$\rho_{nLvJ}(\vec{r})=\left\{[K_{nL}\rho_v(\vec{r},\vec{r}')]_J \right\}_{\vec{r}'=\vec{r}},$$ (38)

which are built by acting with the relative momentum operators $K_{nLM}$ on the scalar ($v=0$) and vector ($v=1$) non-local densities:

$$\rho_{v\mu}\left(\vec{r},\vec{r}\,'\right) = \sum_{\sigma\sigma'}\rho\left(\vec{r}\sigma,\vec{r}\,'\sigma'\right) \left\langle \sigma'\left\vert\sigma_{v\mu}\right\vert\sigma\right\rangle .$$ (39)

Note that the sum in Eq. (38) runs over the indices ordered in a specific way, defined in Ref. [4,5], namely,

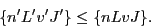$$\{n'L'v'J'\}\leq\{nLvJ\}.$$ (40)

We first vary ${\cal E}$ over the densities and then, in Section 3.3, we vary densities over the wave functions, that is, we begin with

$$\delta{\cal E} = \int {\rm d}^3\vec{r} \delta{\cal H}(\vec{r}) = \sum_{n'L'v'J'M'}\int {\rm d}^3\vec{r} \frac{\partial{\cal H}}{\partial\rho_{n'L'v'J'M'}}(\vec{r})\delta\rho_{n'L'v'J'M'} .$$ (41)

An explicit variation over the primary densities under the differential operators $D_{mI}$ can be avoided by first integrating by parts and recoupling. The recoupling within a scalar [6] is simple, namely,

$$[A_{J'}[B_{I}C_{J}]_{J'}]_0 = (-1)^{J'+I-J} [C_{J}[B_{I}A_{J'}]_{J}]_0.$$ (42)

Hence, the integration by parts gives:

$${\cal H}(\vec{r}) = \sum_{{n'L'v'J'}\atop{mI,nLvJ}} (-1)^{J'+I-J} C^{n'L'v'J'}_{mI,nLvJ}\, [\rho_{nLvJ}(\vec{r})[D^T_{mI}\rho_{n'L'v'J'}(\vec{r})]_J]_0$$

$$= \sum_{{n'L'v'J'}\atop{mI,nLvJ}} (-1)^{m+J'+I-J} C^{n'L'v'J'}_{mI,nLvJ}\, [\rho_{nLvJ}(\vec{r})[D_{mI}\rho_{n'L'v'J'}(\vec{r})]_J]_0$$

$$= \sum_{{n'L'v'J'}\atop{mI,nLvJ}} (-1)^{J-J'} C^{nLvJ}_{mI,n'L'v'J'}\, [\rho_{n'L'v'J'}(\vec{r})[D_{mI}\rho_{nLvJ}(\vec{r})]_{J'}]_0 ,$$ (43)

where we have used Eq. (33), then we changed the names of indices, and we also used the fact that $m+I$ is even.

Therefore, the variation under the differential operators $D_{mI}$ only gives the transposition of indices $\{n'L'v'J'\}\leftrightarrow\{nLvJ\}$ and the phase. The complete variation of the energy then reads:

$$\delta{\cal E} = \sum_{n'L'v'J'}\int {\rm d}^3\vec{r}[\delta\rho_{n'L'v'J'}\tilde{U}_{n'L'v'J'}(\vec{r})]_0 ,$$ (44)

where we defined potentials

$$\tilde{U}_{n'L'v'J'M'}(\vec{r})\!\!\!\! = \sum_{mI,nLvJ}\!\! \left\{C^{n'L'v'J'}_{mI,nLvJ}+(-1)^{J-J'}C^{nLvJ}_{mI,n'L'v'J'}\right\} [D_{mI}\rho_{nLvJ}(\vec{r})]_{J'M'}.$$ (45)

Note that because of the ordering (41), in Eq. (46) either the first or the second term is non-zero (for $\{n'L'v'J'\}\neq\{nLvJ\}$), or both terms add up to $2C^{n'L'v'J'}_{mI,nLvJ}$ (for $\{n'L'v'J'\}=\{nLvJ\}$).