Pairing gaps, separation energies, and halos

A key feature of the nucleonic density $\rho(\mbox{{\boldmath {$r$ }}})$is its second radial moment, i.e., the rms radius $R_{\rm rms}$= $\langle r^2\rangle^{1/2}$. We consider here and in the following the scaled rms radius,

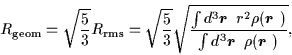$$R_{\rm geom} = \sqrt{\frac{5}{3}}R_{\rm rms} = \sqrt{\f... ...3\mbox{{\boldmath {$r$ }}}\,\rho(\mbox{{\boldmath {$r$ }}})}},$$ (12)

which we call the geometric radius [24]. The factor (5/3)^1/2 serves to bring that value closer to the box radius. Further density characteristics are best deduced from the corresponding form factor

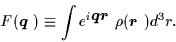$$F(\mbox{{\boldmath {$q$ }}}) \equiv \int e^{i\mbox{{\boldmath {$qr$ }}}}\rho(\mbox{{\boldmath {$r$ }}})d^3r.$$ (13)

For the spherical density distribution $\rho (r)$, the form factor is also spherical and can be expressed in the standard way as $F(q) = \int j_0(qr)\rho(r)r^2dr.$

Good approximation to typical nuclear form factors is given by the Helm model [25,26,27,28,29,30], where nucleonic density is approximated by a convolution of a sharp-surface density of radius R₀ with a Gaussian smoothing profile, i.e,

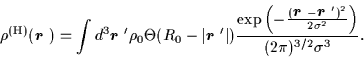$$\rho^{\rm (H)}(\mbox{{\boldmath {$r$ }}}) = \int d^3\mbox... ...ath {$r$ }}}')^2}{2\sigma^2}\right)}} {(2\pi)^{3/2}\sigma^3}.$$ (14)

The quantity R₀ in Eq. (14) is called the diffraction (box equivalent) radius, and the folding width $\sigma$represents the surface thickness. The diffraction radius, R₀, can be deduced from the first zero, q₁, of the microscopic form factor F(q):

 

R₀ = 4.49341/q₁, (15)

while the surface thickness parameter, $\sigma$, can be computed by comparing the values of microscopic and of Helm form factors, F(q_m) and $F^{\rm (H)}(q_m)$, at the first maximum q_m of F(q):

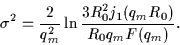$$\sigma^2= \frac{2}{q_m^2}\ln\frac{3R_0^2j_1(q_mR_0)}{R_0q_mF(q_m)}.$$ (16)

The geometric radius of the Helm model can be easily computed as

 

$$R_{\rm Helm} \sqrt{\frac{5}{3}}R^{\rm (H)}_{\rm rms} = \sqrt{\left(R_0^2 +5\sigma^2\right)}.$$ = (17)

From this relation one sees that the geometric radius becomes the box-equivalent radius in the limit of a small surface thickness. The Helm model follows the exact density distribution over a wide range of densities, but some deviations may build up far outside the nucleus at very low densities. Thus the Helm radius is a good approximation to the true geometric radius in well-bound nuclei. The situation changes if one goes towards the drip line where the nucleons become less bound and the outer tail of the density makes a non-negligible contribution to the geometric radius. Since the outer tail is not contained at all in the Helm model, the halo size can be characterized by the difference of these two radii [24], i.e.,

$$\delta{R}_{\rm halo} \equiv R_{\rm geom} - R_{\rm Helm}.$$ (18)

In Ref. [24] it has been shown that $\delta{R}_{\rm halo}$is small in well-bound nuclei, but it becomes enhanced for heavy exotic systems with low neutron separation energies. Furthermore, it was noticed that the halo parameter obtained in the HFB+SLy4 model with DDDI is significantly larger than that predicted in the HFB+SkP model, and in relativistic mean-field models with the finite-range Gogny pairing. In the following, we shall investigate the influence of pairing on $\delta{R}_{\rm halo}$.

The bottom portion of Fig. 6 shows the average neutron pairing gaps [19]

$$\langle\Delta_n\rangle = - \frac{1}{N} \int\mbox{\rm\scrip... ...{\boldmath {$r$ }}}'\sigma',\mbox{{\boldmath {$r$ }}}\sigma).$$ (19)

For $\alpha$=1/6, pairing correlations are so strong that they give rise to a non-zero static pairing in the magic nucleus ¹³²Sn. For larger values of $\alpha$, pairing gaps at 50$\leq$N$\leq$100 are almost independent of $\alpha$, while a weak dependence is seen only near the drip line.

The impact of the pairing Hamiltonian on the two-neutron separation energies in the Sn isotopes is illustrated in Fig. 6, middle portion. The most striking result is that the strong pairing at low densities dramatically reduces the shell effect at N=82. The presence of this effect gives a strong argument against taking small values of $\alpha$when aiming at realistic calculations. Another consequence of enhanced pairing is the shift in the position of the two-neutron drip line, S_2n=0. While for $\alpha$=1 and 1/2 the last two-neutron bound Sn isotope is calculated at N=120; at $\alpha$=1/6 the nuclear binding is increased by pairing and the drip line shifts to N=126.

Finally, the top panel of Fig. 6 displays the neutron halo parameter (18). As already pointed out in Ref. [24], this quantity is very small in well-bound nuclei and increases with decreased separation energy. In the case of Sn isotopes considered, there is a gradual rise of $\delta{R}_{\rm halo}$ for N>132. However, halo size is a very sensitive function of the pairing interaction. Indeed, when decreasing the pairing exponent from $\alpha$=1 to $\alpha$=1/6, the halo parameter increases by an order of magnitude. (Actually, for $\alpha$=1/6, $\delta{R}_{\rm halo}$ is nonzero also for well-bound systems.) This is a consequence of a strong feedback between p-h and p-p densities (cf. discussion around Fig. 2).