Figures

  

Figure 1: Radial strength factor $f_{\rm pair}$ of the density-dependent delta interaction, Eq. (11), as a function of $\rho$for several values of $\alpha$. The value of $\rho _0$ was assumed to be 0.16fm^-3. At each value of $\alpha$, the strength V₀was adjusted to reproduce the neutron pairing gap in ¹²⁰Sn. The inset shows $f_{\rm pair}/\vert V_0\vert$ as a function of dimensionless normalized density $\rho _{\rm IS}/\rho _c$.

  

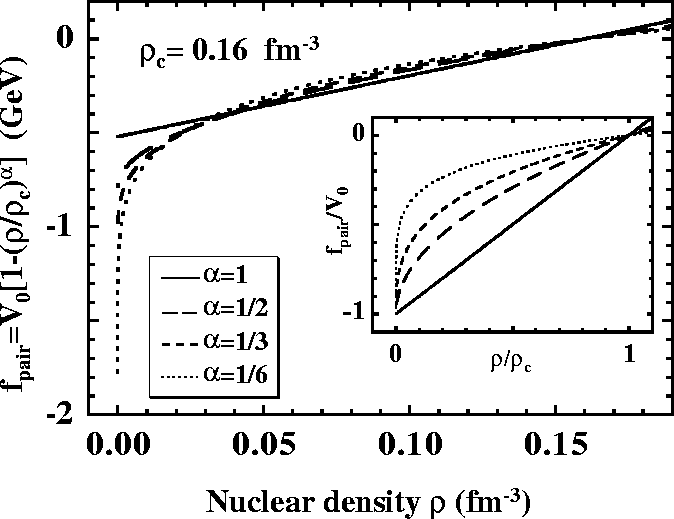Figure 2: Self-consistent spherical HFB+SLy4 local densities $\rho (r)$ (top) and $\tilde{\rho}(r)$ (bottom) for neutrons in ¹⁵⁰Sn for several values of $\alpha$. The insets show the same data in logarithmic scale.

  

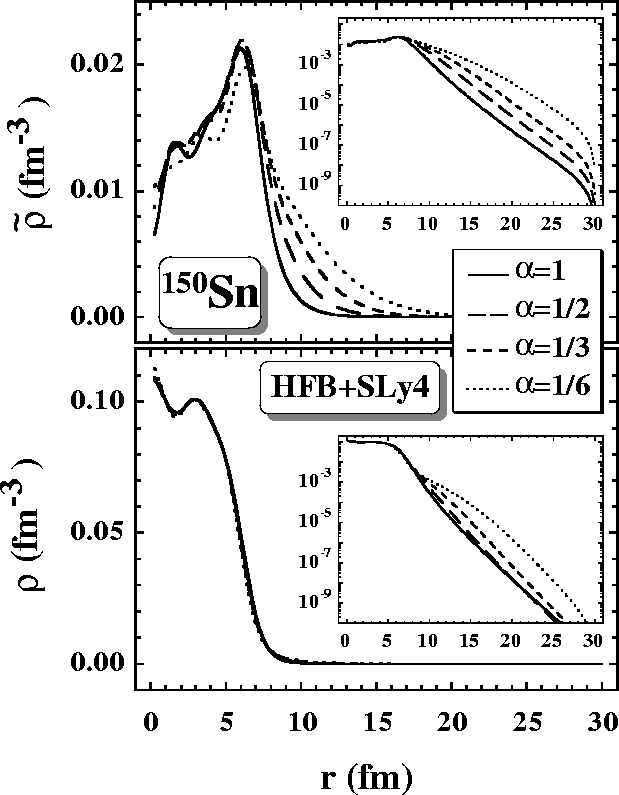Figure 3: Self-consistent spherical HFB+SLy4 local densities $\rho (r)$ (top) and $\tilde{\rho}(r)$ (bottom) for neutrons in ^120,150,170Sn and $\alpha$=1/2. The insets show the same data in logarithmic scale. The dramatic fall-off of densities at 30fm is due to the box boundary conditions.

  

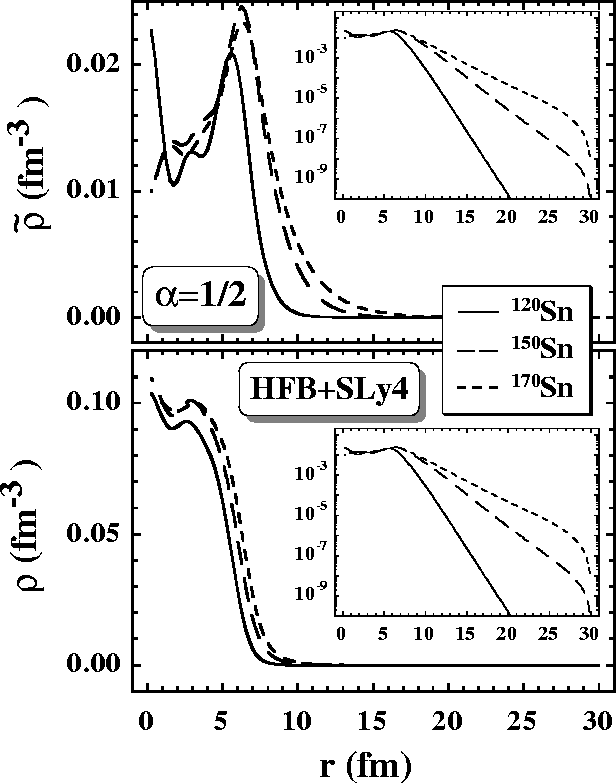Figure 4: Self-consistent spherical HFB+SLy4 local potentials U(r) and $\tilde{U}(r)$ (shown in the inset) for neutrons in ¹⁵⁰Sn for several values of $\alpha$.

  

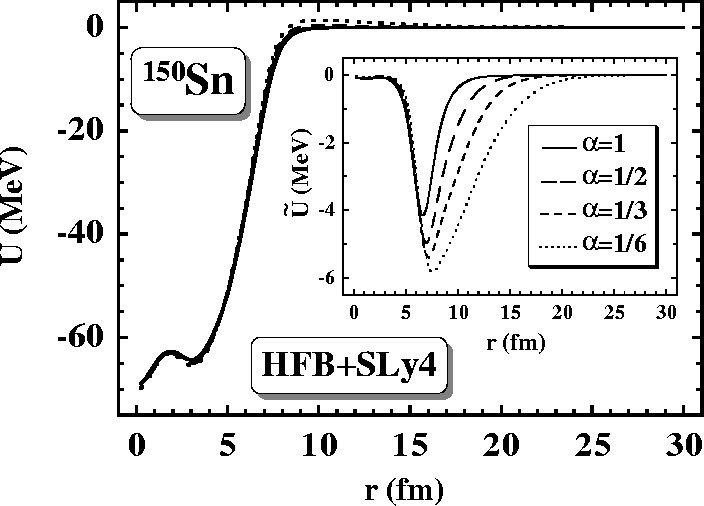Figure 5: Self-consistent spherical HFB+SLy4 local potentials U(r) and $\tilde{U}(r)$ (shown in the inset) for neutrons in ^120,150,170Sn and $\alpha$=1/2.

  

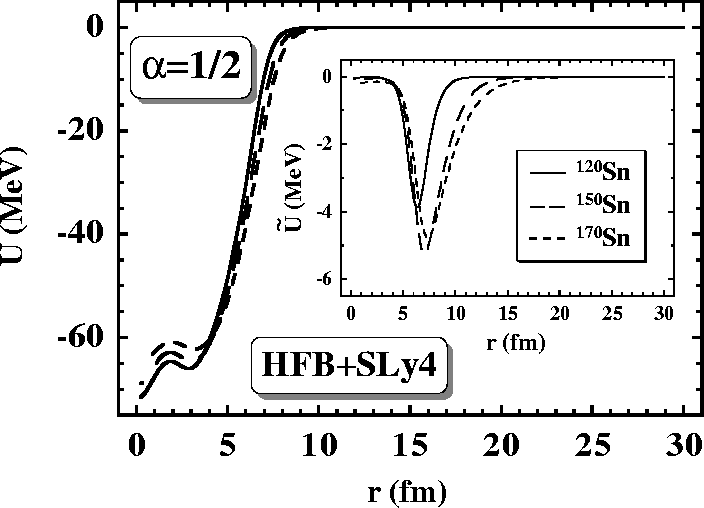Figure 6: Neutron halo parameters (top), two-neutron separation energies (middle), and average neutron pairing gaps (19) calculated in the HFB+SLy4 model with different density-dependent pairing interactions (10).