


Next: conclusions
Up: Continuity equations in the
Previous: Constraints for the vector-isoscalar
Constraints for the vector-isovector channel
Validity of the CE for the vector-isovector density,
Eq. (30) for  and
and  , imposes through
Eq. (48) constraints on the coupling constants that
relate them in both spin and isospin spaces. At all the orders, we
can express all dependent coupling constants through only one vector
coupling constant, which can be chosen either in the set of the
vector-isoscalar or vector-isovector ones. At second order, these
constraints read,
, imposes through
Eq. (48) constraints on the coupling constants that
relate them in both spin and isospin spaces. At all the orders, we
can express all dependent coupling constants through only one vector
coupling constant, which can be chosen either in the set of the
vector-isoscalar or vector-isovector ones. At second order, these
constraints read,
 |
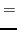 |
 |
(66) |
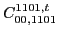 |
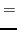 |
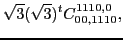 |
(67) |
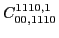 |
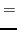 |
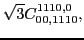 |
(68) |
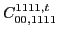 |
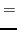 |
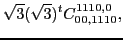 |
(69) |
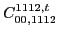 |
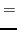 |
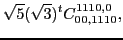 |
(70) |
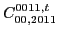 |
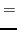 |
 |
(71) |
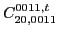 |
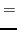 |
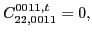 |
(72) |
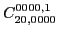 |
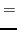 |
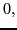 |
(73) |
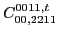 |
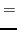 |
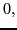 |
(74) |
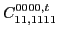 |
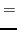 |
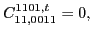 |
(75) |
and only coupling constant
 is unrestricted.
Altogether, at second order for the vector-isovector channel of the
CE we have 2 free coupling constants and 11 coupling constants that
are dependent. All the remaining 11 second-order coupling constants,
which includes the
surface ones in Eqs. (72)-(73), the tensor ones in Eq. (74) and spin-orbit
ones in Eq. (75), are forced to be equal to zero.
is unrestricted.
Altogether, at second order for the vector-isovector channel of the
CE we have 2 free coupling constants and 11 coupling constants that
are dependent. All the remaining 11 second-order coupling constants,
which includes the
surface ones in Eqs. (72)-(73), the tensor ones in Eq. (74) and spin-orbit
ones in Eq. (75), are forced to be equal to zero.
For the fourth and sixth orders, analogous constraints are
presented in Appendix C.



Next: conclusions
Up: Continuity equations in the
Previous: Constraints for the vector-isoscalar
Jacek Dobaczewski
2011-11-11
![]() and
and ![]() , imposes through
Eq. (48) constraints on the coupling constants that
relate them in both spin and isospin spaces. At all the orders, we
can express all dependent coupling constants through only one vector
coupling constant, which can be chosen either in the set of the
vector-isoscalar or vector-isovector ones. At second order, these
constraints read,
, imposes through
Eq. (48) constraints on the coupling constants that
relate them in both spin and isospin spaces. At all the orders, we
can express all dependent coupling constants through only one vector
coupling constant, which can be chosen either in the set of the
vector-isoscalar or vector-isovector ones. At second order, these
constraints read,