


Next: Constraints for the vector-isovector
Up: Continuity equations in the
Previous: Constraints for the scalar-isovector
Constraints for the vector-isoscalar channel
Validity of the CE for the vector-isoscalar density,
Eq. (30) for  and
and  , imposes through
Eq. (48) at second order the following constraints on
the coupling constants of the functional,
, imposes through
Eq. (48) at second order the following constraints on
the coupling constants of the functional,
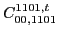 |
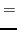 |
 |
(59) |
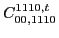 |
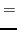 |
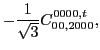 |
(60) |
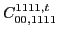 |
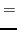 |
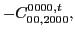 |
(61) |
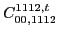 |
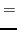 |
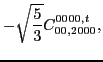 |
(62) |
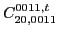 |
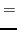 |
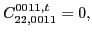 |
(63) |
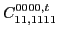 |
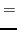 |
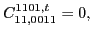 |
(64) |
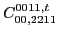 |
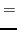 |
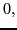 |
(65) |
whereas the two coupling constants
 are left
unrestricted. We note here that the constraints now connect scalar
and vector coupling constants. Altogether, at second order, for the
vector-isoscalar channel of the CE we have 6 free and 8 dependent
coupling constants. Apart from that, 10
second-order coupling constants must vanish, which includes the
surface ones in Eq. (63), spin-orbit ones of the
Eq. (64), and tensor ones in Eq. (65).
are left
unrestricted. We note here that the constraints now connect scalar
and vector coupling constants. Altogether, at second order, for the
vector-isoscalar channel of the CE we have 6 free and 8 dependent
coupling constants. Apart from that, 10
second-order coupling constants must vanish, which includes the
surface ones in Eq. (63), spin-orbit ones of the
Eq. (64), and tensor ones in Eq. (65).
For the fourth and sixth orders, analogous constraints are
presented in Appendix B.



Next: Constraints for the vector-isovector
Up: Continuity equations in the
Previous: Constraints for the scalar-isovector
Jacek Dobaczewski
2011-11-11
![]() and
and ![]() , imposes through
Eq. (48) at second order the following constraints on
the coupling constants of the functional,
, imposes through
Eq. (48) at second order the following constraints on
the coupling constants of the functional,