
Next: Stochastic Gabor dictionaries
Up: A unified parametrization of
Previous: Electroencephalography and science
Matching pursuit (MP) was proposed in [9] and [12]. The former publication by S. Mallat and Z. Zhang was accompanied by a freely available software implementation [8]. Below we briefly recall the basic ideas: we are looking for a linear expansion approximating the analyzed signal s(t):
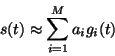 |
(1) |
in terms of functions 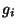 chosen from a large and redundant set (dictionary D). The problem of choosing M functions, which explain the largest part of energy of a given signal, is NP-hard, i.e. computationally intractable. MP offers a sub-optimal solution, obtained by means of an iterative algorithm.
In the first step of the iterative procedure we choose the vector which gives the largest product with the signal. The iterative procedure is repeated on the subsequent residua
chosen from a large and redundant set (dictionary D). The problem of choosing M functions, which explain the largest part of energy of a given signal, is NP-hard, i.e. computationally intractable. MP offers a sub-optimal solution, obtained by means of an iterative algorithm.
In the first step of the iterative procedure we choose the vector which gives the largest product with the signal. The iterative procedure is repeated on the subsequent residua 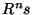 :
:
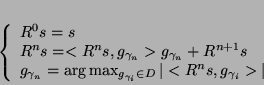 |
(2) |
The procedure converges to 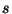
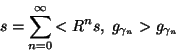 |
(3) |
and conserves signal's energy
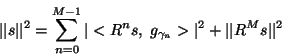 |
(4) |
Subsections


Next: Stochastic Gabor dictionaries
Up: A unified parametrization of
Previous: Electroencephalography and science
Piotr J. Durka
2001-04-04