


Next: Canonical states
Up: Quadrupole deformations of neutron-drip-line
Previous: THO and local densities
Hartree-Fock-Bogoliubov (HFB) theory [20] is based on the Ritz
variational principle applied to the many-fermion Hamiltonian,
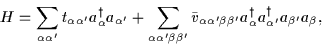 |
(45) |
with trial functions in the form of a
quasiparticle vacuum. The resulting HFB equations can be written in matrix form
as
 |
(46) |
where En are the quasiparticle
energies,  is the chemical potential, and the matrices
is the chemical potential, and the matrices
 and
and
 are defined by the matrix elements of the two-body interaction
are defined by the matrix elements of the two-body interaction
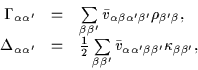 |
(47) |
 and
and
 being the density matrix and pairing tensor, respectively. HFB theory is by now a
standard tool in nuclear structure calculations, and we refer the reader to
Ref. [20] for details. Below we discuss several features of the
formalism that are especially pertinent to the present application, namely
canonical states, the pairing phase space, and those quantities that dictate the
stability of a nucleus with respect to two-neutron emission.
being the density matrix and pairing tensor, respectively. HFB theory is by now a
standard tool in nuclear structure calculations, and we refer the reader to
Ref. [20] for details. Below we discuss several features of the
formalism that are especially pertinent to the present application, namely
canonical states, the pairing phase space, and those quantities that dictate the
stability of a nucleus with respect to two-neutron emission.



Next: Canonical states
Up: Quadrupole deformations of neutron-drip-line
Previous: THO and local densities
Jacek Dobaczewski
1999-09-13