


Next: Properties of the D
Up: Symmetry operators
Previous: Double group D for
Cartesian harmonic oscillator basis
One often uses the Cartesian harmonic oscillator (HO) basis
to solve the self-consistent equations when neither spherical
nor axial symmetry is assumed, see, e.g., Refs. [17,10].
The Cartesian HO states are identified by
the numbers of oscillator quanta, nx, ny, and nz, in the three
Cartesian directions,
and by the spin projection sz=
 on the z axis.
For the standard HO phase convention, this basis is real,
on the z axis.
For the standard HO phase convention, this basis is real,
 ,
where according to our standard
convention the script symbol
,
where according to our standard
convention the script symbol
 denotes the coordinate-space
complex-conjugation operator acting in the odd-fermion-number
space
denotes the coordinate-space
complex-conjugation operator acting in the odd-fermion-number
space
 ,
see Sec. 2.1.
,
see Sec. 2.1.
For the HO states the following relations hold [18]:
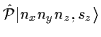 |
= |
 |
(47) |
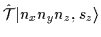 |
= |
 |
(48) |
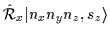 |
= |
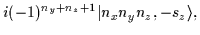 |
(49) |
 |
= |
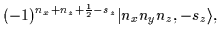 |
(50) |
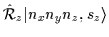 |
= |
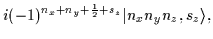 |
(51) |
 |
= |
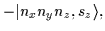 |
(52) |
from where one can find similar equations for all the remaining
operators of group D
 .
Since the HO Hamiltonian
is symmetric under D
.
Since the HO Hamiltonian
is symmetric under D
 ,
its eigenstates can be
classified according to the ircoreps of D
,
its eigenstates can be
classified according to the ircoreps of D
 .
It is easily seen that
the HO states
.
It is easily seen that
the HO states
 form bases of the spinor, pseudospinor,
antispinor and antipseudospinor ircoreps for
form bases of the spinor, pseudospinor,
antispinor and antipseudospinor ircoreps for
 =nx+ny+nz, Ny=nx+
=nx+ny+nz, Ny=nx+ being {even, odd},
{odd, odd}, {even, even} and {odd, even}, respectively (see Appendix). The
entire HO basis would have belonged to the spinor and pseudospinor
ircoreps only, if the basis states and phase convention were chosen differently,
see Ref.[14].
being {even, odd},
{odd, odd}, {even, even} and {odd, even}, respectively (see Appendix). The
entire HO basis would have belonged to the spinor and pseudospinor
ircoreps only, if the basis states and phase convention were chosen differently,
see Ref.[14].



Next: Properties of the D
Up: Symmetry operators
Previous: Double group D for
Jacek Dobaczewski
2000-02-05
![]() on the z axis.
For the standard HO phase convention, this basis is real,
on the z axis.
For the standard HO phase convention, this basis is real,
![]() ,
where according to our standard
convention the script symbol
,
where according to our standard
convention the script symbol
![]() denotes the coordinate-space
complex-conjugation operator acting in the odd-fermion-number
space
denotes the coordinate-space
complex-conjugation operator acting in the odd-fermion-number
space
![]() ,
see Sec. 2.1.
,
see Sec. 2.1.