Quasi-Particle Excitations in Rotating Neutron-Rich Nuclei

Nuclear high-spin behavior is always strongly impacted by the single-particle shell structure. The order of single-particle states around the Fermi level determines the deformability of the nucleus, its moment of inertia, and the Coriolis coupling. Consequently, any changes to the shell structure are going to show up at high spins. In this section, we discuss several signatures of shell quenching as seen through the quasi-particle spectra of rotating nuclei.

The major consequence of the modified shell structure in neutron-rich nuclei is the change in the placement of unique-parity orbitals which revert to their original shells. Since high-j states are the building blocks of nuclear rotation (they are influenced most by the Coriolis coupling), this shift is expected to impact a number of observables. In order to illustrate the effect of shell quenching on nuclear rotation, we performed the deformed shell-model analysis of quasi-neutron spectra in extremely neutron-rich deformed nuclei. According to recent Skyrme-HFB calculations [47], the largest deformations in heavy neutron drip-line nuclei are expected in three regions: around ¹⁰⁰Zn, ¹⁴⁶Pd, and in the Rare Earths (Gd, Dy, Er, and Yb). It is to be noted that the microscopic-macroscopic finite range droplet model [48] also predicts deformations in these regions.

  

Figure 3: Energy difference between the spherical j_15/2 level and the centers of gravity of the $\cal{N}$ = 6 and $\cal{N}$=7 shells as a function of the neutron diffuseness parameter ain the spherical WS potential. Calculations were performed for ²⁰⁸Er.

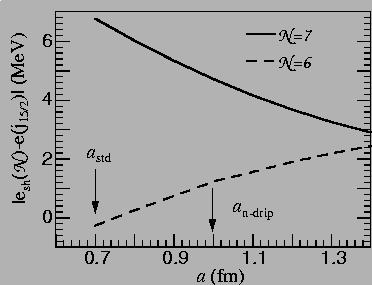Figure 3 displays the energy difference between the spherical j_15/2 level and the centers of gravity, $e_{sh}(\cal{N})$, of the normal-parity $\cal{N}$=6 and $\cal{N}$=7 shells as a function of a. At the standard value of a=0.7fm, the j_15/2 level lies close to the center of the $\cal{N}$=6 shell, and almost 1 $\hbar \omega_0$ below the $\cal{N}$=7 shell. With increasing a, the intruder shell gradually moves towards the $\cal{N}$=7 shell. We checked that the inclusion of deformation does not change this pattern.

The calculations were performed with the cranked Woods-Saxon (WS) model with the constant pairing gap approximation [49,50]. In order to mock up the self-consistent spectra, the WS neutron diffuseness parameter a has been varied in order to reproduce the behavior of spherical single-neutron levels obtained in HFB. For the details of the calculations, we refer the reader to Ref. [51].

  

Figure 4: Decoupling parameters of the [770]1/2 and [660]1/2 levels (top) and the quasi-particle alignments of the lowest $\cal{N}$ = 6 and $\cal{N}$=7 quasi-particle Routhians (at $\hbar\omega$=0.1MeV, bottom) as functions of the neutron diffuseness of parameter. Calculations were performed at $\beta_2$=0.25 and $\Delta$=1MeV.

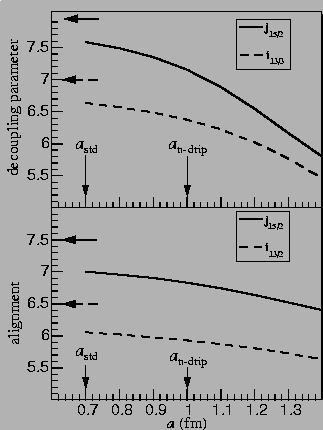The effect of the large diffuseness on the rotational properties of high-j states is rather weak. Figure 4 (top) displays the decoupling parameters of the [770]1/2 and [660]1/2 Nilsson levels as a functions of a. Although the decoupling parameters do decrease with the diffuseness, for the realistic values of a, they are still fairly close to the pure single-j limits of j+1/2 indicated by arrows in Fig. 4. As is seen in Fig. 4 (bottom), the effect on the quasi-particle alignment is even weaker.

  

Figure 5: Quasi-particle neutron diagram calculated in the WS model for two N=140 isotones: ²³⁰Th and ²⁰⁸Er. Calculations were performed at $\beta_2$=0.25 and $\Delta$=1MeV.

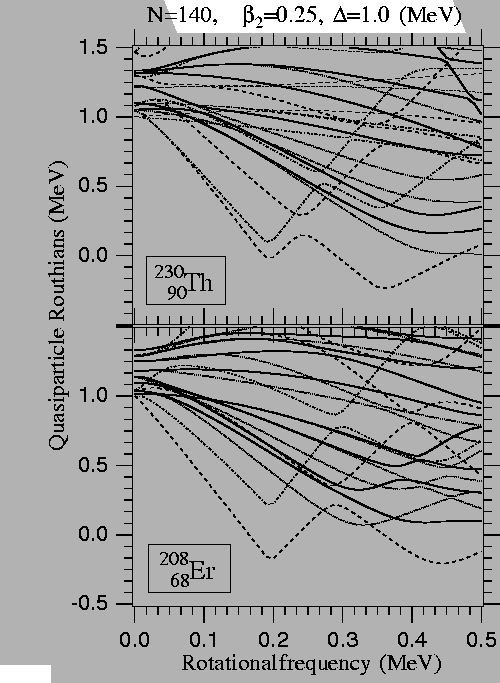It is the pattern of quasi-particle excitations where more deviations from the standard situation are expected. Consider, e.g., two N=140 isotones: ²³⁰Th and the very neutron-rich nucleus ²⁰⁸Er. In the case of ²³⁰Th, the neutron Fermi level lies between the $\Omega$=5/2 and $\Omega$=7/2 members of the j_15/2 shell. In ²⁰⁸Er, due to increased diffuseness, the intruder shell moves up (cf. Fig. 3) and the neutron Fermi level lies at the bottom of the shell, i.e., in the vicinity of the [770]1/2 Nilsson level. As seen in Fig. 5, this changes the signature splitting of the lowest negative parity states and also the position of the higher-frequency neutron crossings. A similar situation is expected around ¹⁴⁶Pd, where the i_13/2 intruder is shifted up in energy.