The Lipkin operator

A practical method to calculate the correcting constant $k$ from Eq. (18) must not involve, of course, the exact evaluation of the function $E_\Phi(\bm{P})$. A method to probe the function $E_\Phi(\bm{P})$ without evaluating it explicitly can be formulated as follows. One first remarks that the projected energy (4) can also be calculated as:

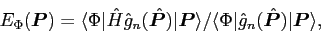$$E_\Phi(\bm{P}) = {\langle\Phi\vert\hat{H}\hat{g}_n(\hat{\bm{... ...{\langle\Phi\vert \hat{g}_n(\hat{\bm{P}})\vert\bm{P}\rangle} ,$$ (20)

which gives the sum rules:

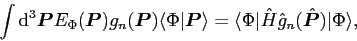$$\int {\rm {d}}^3 \bm{P} E_\Phi(\bm{P}){g}_n(\bm{P}){\langle\... ...angle\Phi\vert\hat{H}\hat{g}_n(\hat{\bm{P}})\vert\Phi\rangle ,$$ (21)

where $\hat{g}_n(\hat{\bm{P}})$ are arbitrary functions of $\hat{\bm{P}}$. By using different functions $\hat{g}_n$, one can probe the unknown function $E_\Phi(\bm{P})$.

An obvious choice of $\hat{g}_n=\hat{\bm{P}}^{2n}$, which, in fact, has been used within the Lipkin-Nogami method [7] to restore the particle number, requires dealing with impractical many-body operators. A much better option is provided by the shift operators [cf. Eq. (1) and (2)],

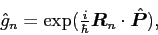$$\hat{g}_n = \exp({\textstyle{\frac{i}{\hbar}}}\bm{R}_n\cdot\hat{\bm{P}}) ,$$ (22)

defined for a suitably selected values of shifts $\bm{R}_n$. Then, the average values on the right-hand side of Eq. (21) become equal to the energy kernels $H(\bm{R}_n)$, which are very easy to calculate.

In practice, the method works as follows. Suppose one wants to evaluate the Taylor-expansion coefficients of $E_\Phi(\bm{P})$ up to a given order of $2M$,

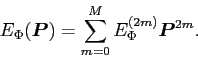$$E_\Phi(\bm{P}) = \sum_{m=0}^M E_\Phi^{(2m)} \bm{P}^{2m}.$$ (23)

After inserting this into Eq. (21), one obtains the set of linear equations,

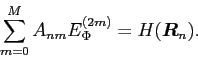$$\sum_{m=0}^M A_{nm} E_\Phi^{(2m)} = H(\bm{R}_n).$$ (24)

where the matrix $A_{nm}$ is defined by the kernels of the momentum operators:

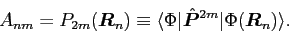$$A_{nm} = {P}_{2m}(\bm{R}_n) \equiv \langle\Phi\vert{\hat{\bm{P}}}^{2m}\vert\Phi(\bm{R}_n)\rangle .$$ (25)

In the simplest case of the quadratic Lipkin operator, Eq. (14), one only needs the expansion up the second order, that is, for $M=1$. Then, by using two points $\bm{R}_0\equiv\bm{0}$ and $\bm{R}_1\equiv\bm{R}$ one obtains

$$A = \left(\begin{array}{ccc} 1&,& \langle\Phi\vert{\hat{\bm{... ...hat{\bm{P}}}^{2}\vert\Phi(\bm{R})\rangle \end{array}\right) .$$ (26)

This matrix can be easily inverted and then one obtains the first two Taylor expansion coefficients $E_\Phi^{(0)}$ and $E_\Phi^{(2)}$, which are required in Eq. (18), that is,

$$E_\Phi(\bm{0}) = \frac{h(\bm{0})p_2(\bm{R})-h(\bm{R})p_2(\bm{0})} {p_2(\bm{R})-p_2(\bm{0})} ,$$ (27)

$$k = \frac{h(\bm{R})-h(\bm{0})} {p_2(\bm{R})-p_2(\bm{0})} ,$$ (28)

where the reduced kernel of the momentum operator is defined as usually, by $p_2(\bm{R})=P_2(\bm{R})/I(\bm{R})$. Expressions (27) and (28) can be very easily evaluated, especially in view of the fact that the momentum kernel can be calculated as a Laplacian of the overlap kernel:

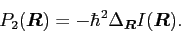$$P_2(\bm{R}) = -\hbar^2 \Delta_{\bm{R}} I(\bm{R}).$$ (29)

Of course, within the GOA, the results are exactly the same as those given by the zero-point-motion correction and PY mass, Eqs. (10) and (11). However, expressions (27) and (28) do not rely on the GOA. They only depend on assuming the quadratic form of the Lipkin operator $\hat{K}$, Eq. (14). Moreover, variations of explicit expressions for the projected energy $E_\Phi(\bm{0})$, like the ones given by Eqs. (9) or (27), are difficult, while that of the Lipkin projected energy (19) can be carried out by the standard self-consistent procedure.

When the quadratic approximation is not sufficient, one can immediately notice this fact by a dependence of $E_\Phi(\bm{0})$ and $k$ on the value of the shift $\bm{R}$. In this case, one can always switch to higher-order Lipkin operators:

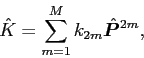$$\hat{K}=\sum_{m=1}^M k_{2m}\hat{\bm{P}}^{2m},$$ (30)

which would require using higher-order Taylor expansions (23), and $M$ different shifts $\bm{R}_n$, $n=1,\ldots,M$, instead of one. The only requirement for choosing the shifts $\bm{R}_n$ is a non-singularity of the matrix $A$. A dependence of the results on this choice will always give a signal that a given order is insufficient. Note that kernels of higher powers of the momentum operator can also be calculated in terms of higher derivatives of the overlap kernel, in analogy with Eq. (29). However, in view of the fact that for the translational symmetry the GOA works so nicely, in this study there does not seem to be any immediate necessity to go to higher orders, and the simple quadratic correction will suffice.

Figure 5: (Color online) The Lipkin projected energies (19) calculated in 9 doubly-magic spherical nuclei, and plotted relative to the standard energies calculated for the SLy4 Skyrme functional [9]. Open and full squares show results obtained for the exact [$k=\hbar^2/2mA$] and calculated [Eq. (28)] correcting factors, respectively. Solid line shows the fit of the volume and surface terms.

Figure 6: (Color online) Exact masses ($M=mA$, open squares) and the PY masses calculated after the Lipkin minimization from Eq. (28) ($M=\hbar^2/2k$, full squares), compared with the PY masses of Fig. 4 (full circles).