


Next: The Lipkin method
Up: Results
Previous: Kernels
Projected energies
Within the GOA, the Fourier transforms above can be analytically
calculated, and the projected energy of Eq. (4) reads [1]
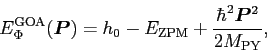 |
(9) |
where the so-called zero-point-motion correction and Peierls-Yoccoz (PY)
mass are given by
For completeness, in Figs. 3 and 4, I show the mass
dependence of the GOA parameters  ,
,  ,
,
 , and
, and
 , along with the fits of the power-law dependencies. One
clearly sees that the PY mass is not equal to the total mass
, along with the fits of the power-law dependencies. One
clearly sees that the PY mass is not equal to the total mass  of
the nucleus. However, as discussed below, it is the PY mass, and not
the physical mass
of
the nucleus. However, as discussed below, it is the PY mass, and not
the physical mass  , which is important for the
translational-symmetry restoration.
, which is important for the
translational-symmetry restoration.
Figure 3:
(Color online) Dots show parameters  (bottom) and
(bottom) and  (top) that
are calculated by the parabolic fits to the logarithms of the overlap
kernels (Fig. 1) and reduced energy kernels
(Fig. 2). Lines give estimates of the power-law
dependence.
(top) that
are calculated by the parabolic fits to the logarithms of the overlap
kernels (Fig. 1) and reduced energy kernels
(Fig. 2). Lines give estimates of the power-law
dependence.
![\includegraphics[angle=0,width=0.7\columnwidth]{renmas.fig3.eps}](img46.png) |
Figure 4:
(Color online) The GOA zero-point-motion corrections
 and PY masses
and PY masses
 (inset) calculated for the values of
parameters
(inset) calculated for the values of
parameters  and
and  that are shown in Fig. 3.
that are shown in Fig. 3.
![\includegraphics[angle=0,width=0.7\columnwidth]{renmas.fig4.eps}](img49.png) |
The average energy of the system at rest,
 , depends
on the Slater determinant
, depends
on the Slater determinant  , and in what follows we are
interested in minimizing this energy with respect to
, and in what follows we are
interested in minimizing this energy with respect to  ,
that is, in performing the VAP or variation after
symmetry restoration.
To this end, in this study I follow the seminal idea by Harry Lipkin
[6], who realized that the VAP calculations can be very
easily performed by flattening the function
,
that is, in performing the VAP or variation after
symmetry restoration.
To this end, in this study I follow the seminal idea by Harry Lipkin
[6], who realized that the VAP calculations can be very
easily performed by flattening the function
 .
.
Indeed, from Eqs. (3) and (4) one obtains the so-called
sum-rule property,
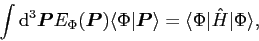 |
(12) |
which tells us that the MF energy
 is equal to the average of the
projected energies
is equal to the average of the
projected energies
 weighted by amplitudes
weighted by amplitudes
 . Therefore, minimization of
. Therefore, minimization of
 , that is, the standard MF
method, corresponds to an entangled minimization of both the
projected energies
, that is, the standard MF
method, corresponds to an entangled minimization of both the
projected energies
 and amplitudes
and amplitudes
 , whereas the VAP method pertains to the
minimization of the energy
, whereas the VAP method pertains to the
minimization of the energy
 only, and, of course,
disregards the amplitudes
only, and, of course,
disregards the amplitudes
 completely.
completely.
Note that the GOA amplitudes
 are all
positive,
are all
positive,
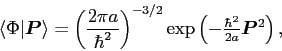 |
(13) |
and hence the MF minimization is bound to underestimate the momentum
spread of the Slater determinant. It is then obvious that unless the
center-of-mass and internal degrees of freedom are exactly separated,
like is the case for the closed-shell HO
[11,12,13] or for the coupled-cluster states
[14], the MF and VAP Slater determinants can be different.



Next: The Lipkin method
Up: Results
Previous: Kernels
Jacek Dobaczewski
2009-06-28
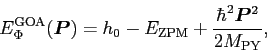
![]() ,
, ![]() ,
,
![]() , and
, and
![]() , along with the fits of the power-law dependencies. One
clearly sees that the PY mass is not equal to the total mass
, along with the fits of the power-law dependencies. One
clearly sees that the PY mass is not equal to the total mass ![]() of
the nucleus. However, as discussed below, it is the PY mass, and not
the physical mass
of
the nucleus. However, as discussed below, it is the PY mass, and not
the physical mass ![]() , which is important for the
translational-symmetry restoration.
, which is important for the
translational-symmetry restoration.
![\includegraphics[angle=0,width=0.7\columnwidth]{renmas.fig3.eps}](img46.png)
![\includegraphics[angle=0,width=0.7\columnwidth]{renmas.fig4.eps}](img49.png)
![]() , depends
on the Slater determinant
, depends
on the Slater determinant ![]() , and in what follows we are
interested in minimizing this energy with respect to
, and in what follows we are
interested in minimizing this energy with respect to ![]() ,
that is, in performing the VAP or variation after
symmetry restoration.
To this end, in this study I follow the seminal idea by Harry Lipkin
[6], who realized that the VAP calculations can be very
easily performed by flattening the function
,
that is, in performing the VAP or variation after
symmetry restoration.
To this end, in this study I follow the seminal idea by Harry Lipkin
[6], who realized that the VAP calculations can be very
easily performed by flattening the function
![]() .
.
![]() are all
positive,
are all
positive,