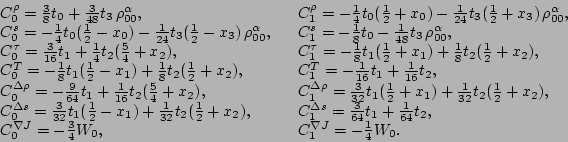Next: Bibliography
Up: Interaction matrix elements (second
Previous: Representation of second derivatives
To calculate the coupled matrix elements in Eqs. (23)-(25),
we use an intermediate LS scheme:
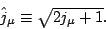 |
(47) |
Eq. (38) gives
i) proton-proton or neutron-neutron matrix elements:
ii) proton-neutron matrix elements:
We use the canonical (and real) radial wave functions  , the
angular wave functions
, the
angular wave functions
 , and the
spin wave functions
to write the nontrivial matrix elements included in Eqs. (49) and (50) as
, and the
spin wave functions
to write the nontrivial matrix elements included in Eqs. (49) and (50) as
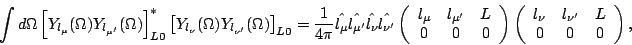 |
(50) |
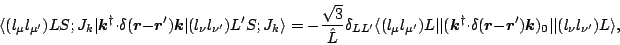 |
(52) |
The square brackets around products of spherical harmonics and the
parentheses surrounding products of operators indicate
angular-momentum coupling.
To evaluate Eqs. (54) and (55), one can use
where for reduced matrix elements we have used the convention
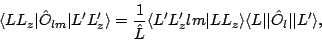 |
(55) |
and made the abbreviation
Eq. (51), modified to include additional factors in
the radial integral, can also be used (together with the subsequent equations)
to evaluate the matrix elements of the terms involving
 in
in
 , the
Coulomb-exchange interaction, and the contributions of the pairing functional
to the effective ph, pp, and 3p1h interactions.
The Coulomb-direct term can be evaluated in a similar but slightly more
complicated way, via a multipole expansion.
, the
Coulomb-exchange interaction, and the contributions of the pairing functional
to the effective ph, pp, and 3p1h interactions.
The Coulomb-direct term can be evaluated in a similar but slightly more
complicated way, via a multipole expansion.
In the main part of this paper we used the Skyrme
functional SkM , which is usually parameterized as in interaction in
terms of coefficients
, which is usually parameterized as in interaction in
terms of coefficients
 and
and  .
The relations between these coefficients and those used here, if no terms
are neglected, are [79,63]
.
The relations between these coefficients and those used here, if no terms
are neglected, are [79,63]
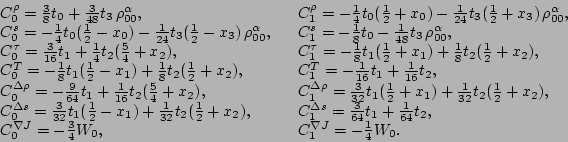 |
(57) |
In the HF fits that originally determined the SkM parameters, the effects of
parameters, the effects of  (the ``
(the `` terms'') were
neglected because of technical difficulties. These terms have often been
included in subsequent RPA calculations. To maintain self consistency here,
we have
set them to zero both
in the HFB calculation and in the QRPA.
terms'') were
neglected because of technical difficulties. These terms have often been
included in subsequent RPA calculations. To maintain self consistency here,
we have
set them to zero both
in the HFB calculation and in the QRPA.



Next: Bibliography
Up: Interaction matrix elements (second
Previous: Representation of second derivatives
Jacek Dobaczewski
2004-07-29


![$\displaystyle -\frac{1}{4}\delta_{LL^\prime}
\int d\Omega \left[ Y_{l_\mu}(\Ome...
...ight]^\ast_{L0}
\left[ Y_{l_\nu}(\Omega) Y_{l_{\nu^\prime}}(\Omega)\right]_{L0}$](img344.png)
![$\displaystyle \times \int dr\:r^2 R_\mu(r) R_{\mu^\prime}(r)
\left\{ \left[ \le...
...}{dr}-\frac{l_\nu(l_\nu+1)}{r^2}
\right)R_\nu(r)\right]R_{\nu^\prime}(r)\right.$](img345.png)
![$\displaystyle \left.+R_\nu(r)\left[ \left( \frac{d^2}{dr^2}+\frac{2}{r}\frac{d}...
...{l_{\nu^\prime}(l_{\nu^\prime}+1)}{r^2}\right)R_{\nu^\prime}(r)
\right]\right\}$](img346.png)



![$\displaystyle \times
\delta_{LL^\prime}
\int d\Omega \left[ Y_{l_\mu}(\Omega)
Y...
...Delta l_{\nu^\prime} }(\Omega)
Y_{l_\nu-1+2\Delta l_\nu} (\Omega)\right]_{L0} ,$](img350.png)




![$\displaystyle \times
\left.
\left( \begin{array}{ccc}l_\nu +2\Delta l_\nu-1 & l...
...arrow \nu^\prime]
-(-)^{l_\mu+l_{\mu^\prime}+L}[\mu \leftrightarrow \mu^\prime]$](img360.png)
![]() in
in
![]() , the
Coulomb-exchange interaction, and the contributions of the pairing functional
to the effective ph, pp, and 3p1h interactions.
The Coulomb-direct term can be evaluated in a similar but slightly more
complicated way, via a multipole expansion.
, the
Coulomb-exchange interaction, and the contributions of the pairing functional
to the effective ph, pp, and 3p1h interactions.
The Coulomb-direct term can be evaluated in a similar but slightly more
complicated way, via a multipole expansion.
![]() , which is usually parameterized as in interaction in
terms of coefficients
, which is usually parameterized as in interaction in
terms of coefficients
![]() and
and ![]() .
The relations between these coefficients and those used here, if no terms
are neglected, are [79,63]
.
The relations between these coefficients and those used here, if no terms
are neglected, are [79,63]